Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height of the flagstaff. [use √3=1.73]
उत्तर
Solution:
Let AB is the tower of height h meter and AC is flagstaff of height x meter.
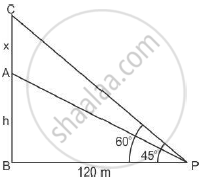
∠APB=45° and ∠BPC =60°
`Tan 60 = (x+h)/120`
`sqrt3=(x+h)/120`
`x=120sqrt3-h`
`tan 45=h/120`
therefore height of the flagstaff =
`=120sqrt3-120`
`=120(sqrt3-1)`
`=120 xx73`
`=87.6 cm`
APPEARS IN
संबंधित प्रश्न
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are 60° and 30° respectively. Find the height of the tower.
If the elevation of the sun changed from 30º to 60º, then find the difference between the lengths of shadows of a pole 15 m high, made at these two positions
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

The shadow of a tower standing on a level ground is found to be 40 m longer when Sun’s altitude is 30° than when it was 60°. Find the height of the tower.
A man sitting at a height of 20 m on a tall tree on a small island in the middle of a river observes two poles directly opposite to each other on the two banks of the river and in line with the foot of the tree. If the angles of depression of the feet of the poles from a point at which the man is sitting on the tree on either side of the river are 60° and 30°respectively. Find the width of the river.
The angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation of the top is 45°. Calculate the height of the tower.
A boy standing at a distance of 48 meters from a building observes the top of the building and makes an angle of elevation of 30°. Find the height of the building.
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
The tops of two poles of height 16 m and 10 m are connected by a wire of length lmetres. If the wire makes an angle of 30° with the horizontal, then l =
An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37°. After what period of time does the angle of elevation increase to 53°? (tan 53° = 1.3270, tan 37° = 0.7536)
