Advertisements
Advertisements
Question
The angle of elevation of a cloud from a point h metre above a lake is θ. The angle of depression of its reflection in the lake is 45°. The height of the cloud is
Options
h tan (45° + θ)
h cot (45° − θ)
h tan (45° − θ)
h cot (45° + θ)
Solution
Let AB be the surface of the lake and p be the point of observation. So AP=h . The given situation can be represented as,
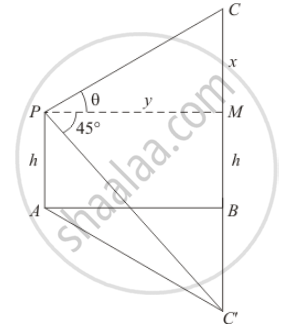
Here,C is the position of the cloud and C' is the reflection in the lake. Then .`CB=C'B`
Let PM be the perpendicular from P on CB. Then `∠CPM=θ` and .`∠C'PM=45°`
Let`CM=x` , `PM=y` , then`CB=x+h` and `C'B=x+h`
Here, we have to find the height of cloud.
So we use trigonometric ratios.
In , `ΔCMP`
`⇒ tan θ=(CM)/(PM)`
`⇒ tanθ=x/y`
`⇒ y= x/tanθ ` (1)
Again in ΔPMC',
`⇒ tan 45°=CM/PM`
`⇒1=(C'B+BM)/(PM)`
`⇒1=(x+h+h)/y`
`⇒y=x+2h`
`⇒ x/tanθ=x+2h` [using (1)]
`⇒ (x-x tanθ)/tan θ=2h`
`⇒ x=(2h tan θ)/((1-tan θ))`
Now,
`⇒ CB=h+x`
`⇒ CB=h+(2h tan θ)/(1-tan θ)`
`⇒ CB=(h(1-tanθ)+2h tanθ)/(1-tan θ)`
`⇒ CB= (h(1+tan θ))/(1-tan θ)=h tan(45°+ θ )` `[tan (A+B)=(tan A+tan B)/(1-tan A tan B)] `
APPEARS IN
RELATED QUESTIONS
If the angle of elevation of a cloud from a point h metres above a lake is α and the angle of depression of its reflection in the lake is β, prove that the height of the cloud is
`\frac{h(\tan\alpha +\tan \beta )}{\tan \beta -\tan \alpha }`
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
From the top of the tower h metre high , the angles of depression of two objects , which are in the line with the foot of the tower are ∝ and ß (ß> ∝ ) cts .
The angle of elevation of the top of a tower at a point on the ground is 30º. What will be the angle of elevation, if the height of the tower is tripled?
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
A tree is broken by the wind. The top struck the ground at an angle of 30° and at a distance 30 m from the root. Find the whole height of the tree. (`sqrt(3)`=1.73)
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find radius of the dome `(sqrt(3) = 1.732)`
The angles of elevation of the top of the rock from the top and foot of 100 m high tower are respectively 30° and 45°. The height of the rock is ____________.
An observer `sqrt3` m tall is 3 m away from the pole `2 sqrt3` high. What is the angle of elevation of the top?
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top remains unchanged.
