Advertisements
Advertisements
Question
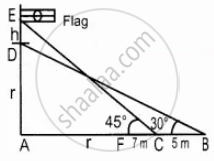
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find radius of the dome `(sqrt(3) = 1.732)`
Solution
Height of the Flag pole (ED) = h m
AF and AD is the radius of the semi circle (r)
AC = (r + 7)
AB = (r + 7 + 5)
= (r + 12)
In the right ∆ABD, tan 30° = `"AD"/"AB"`
`1/sqrt(3) = r/("r" + 12)`
`sqrt(3` r = r + 12
`sqrt(3)` r − r = 12
⇒ `"r" (sqrt(3) - 1)` = 12
r[1.732 – 1] = 12
⇒ 0.732r = 12
r = `12/(0.732)` ⇒ = 16.39 m
In the right ∆ACE, tan 45° = `"AE"/"AC"`
`1 + ("r" + "h")/("r" + 7)`
r + 7 = r + h
∴ h = 7 m
Radius of the dome (r) = 16.39 m
APPEARS IN
RELATED QUESTIONS
The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds the angle of elevation becomes 300 If the aeroplane is flying at a constant height of 3000 3 m, find the speed of the aeroplane.
If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is
`(h (tan ∝+tan ß))/ (tan ∝+tan ∝)`
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is B to the West of A?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is `200[(sqrt(3) + 1)/sqrt(3)]` metres, find the height of the lighthouse.
The angle of elevation of the top of a tower from certain point is 30°. If the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower.
A pole of height 30 m is observed from a point. The angle of depression of the point is 30°. Find the distance of the point from the base of the pole.
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is ______.
