Question

The top of a 15 m high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?

Answer 1

Let the height of the electric pole AD be “h” m

EC = 15 – h m

Let AB be “x”

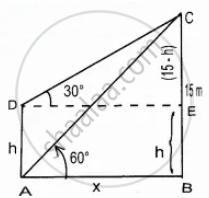
In the right ∆ABC, tan 60° = `"BC"/"AB"`

`sqrt(3) = 15/x`

x = `15/sqrt(3)`

= `(15 xx sqrt(3))/3`

= `5sqrt(3)`

In the right ∆CDE, tan 30° = `"EC"/"DE"`

`1/sqrt(3) = (15 - "h")/x`  ...(1)

Substitute the value of x = `5sqrt(3)` in (1)

`1/sqrt(3) = (15 - "h")/(5sqrt(3))`

⇒ `sqrt(3)(15 - "h") = 5sqrt(3)`

(15 – h) = `(5sqrt(3))/sqrt(3)`

⇒ 15 – h = 5

h = 15 – 5 = 10
∴ Height of the electric pole = 10 m