Advertisements
Advertisements
Question
The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds the angle of elevation becomes 300 If the aeroplane is flying at a constant height of 3000 3 m, find the speed of the aeroplane.
Solution
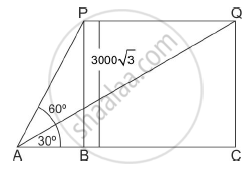
Let P and Q be the two positions of the plane and A be the point of observation. Let ABC be the horizontal line through A.
It is given that angles of elevation of the plane in two positions P and Q from a point A are 60° and 30° respectively.
∠PAB = 60°, ∠QAB = 30°. It is also given that PB = 3000√3 meters
In ΔABP, we have
`tan 60="BP"/"AB"`
`sqrt3/1=(3000sqrt3)/"AB"`
AB=3000m
In ΔACQ, we have
`tan 30="QC"/"AC"`
`1/sqrt3=(3000sqrt3)/"AC"`
AC = 9000 m
∴ Distance = BC = AC – AB = 9000m – 3000m = 6000m
Thus, the plane travels 6km in 30 seconds
Hence speed of plane = 6000/30 = 200 m/sec = 720km/h
APPEARS IN
RELATED QUESTIONS
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x, y.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall is
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
From the top of a tree of height 13 m the angle of elevation and depression of the top and bottom of another tree are 45° and 30° respectively. Find the height of the second tree. `(sqrt(3) = 1.732)`
A building and a statue are in opposite side of a street from each other 35 m apart. From a point on the roof of building the angle of elevation of the top of statue is 24° and the angle of depression of base of the statue is 34°. Find the height of the statue. (tan 24° = 0.4452, tan 34° = 0.6745)
An observer `sqrt3` m tall is 3 m away from the pole `2 sqrt3` high. What is the angle of elevation of the top?
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun ____________.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite bank of the river is 60° and when he retires 40 meters away from the tree the angle of elevation becomes 30°. The breadth of the river is ______.
