Advertisements
Advertisements
Questions
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
From the top of a 7 m high building, the angle of elevation of the top of a tower is 60° and the angle of depression of its foot is 45°. Find the height of the tower.
Solution 1
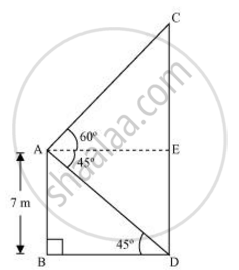
Let AB be a building and CD be a cable tower.
In ΔABD,
`"AB"/"BD"` = tan 45°
`7/"BD"` = 1
BD = 7 m
In ΔACE,
AE = BD = 7 m
`"CE"/"AE"` = tan 60°
`"CE"/7 = sqrt3`
`"CE" = 7sqrt3 "m"`
CD = CE + ED
= `(7sqrt3 + 7)"m"`
= `7(sqrt3 + 1)"m"`
Therefore, the height of the cable tower is `7(sqrt3+1)"m"`.
Solution 2
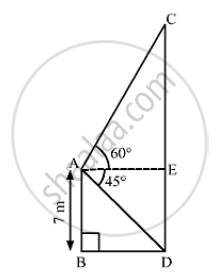
Let AB be the 7m high building and CD be the cable tower,
We have,
AB = 7 m, ∠CAE = 60°, ∠DAE = ∠ADB = 45°
Also, DE = AB = 7 m
In ΔABD,
tan 45° = `("AB")/("BD")`
⇒ 1 = `7/("BD")`
⇒ BD = 7 m
So, AE = BD = 7m
Also, In ΔACE,
tan 60° = `("CF")/("AE")`
⇒ `sqrt(3) = ("CE")/7`
⇒ CE = `7sqrt(3)"m"`
Now, CD = CE + DE
= `7 sqrt(3) +7`
= `7 (sqrt(3) +1) "m"`
= 7(1.732 + 1)
= 7(2.732)
= 19.124
= 19.12 m
So, the height of the tower is 19.12 m.
APPEARS IN
RELATED QUESTIONS
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are 60° and 30° respectively. Find the height of the tower.
A 21 m deep well with diameter 6 m is dug and the earth from digging is evenly spread to form a platform 27 m ✕ 11 m. Find the height of the platform.[Use `pi=22/7`]
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If height of the tower is 50 m, find the height of the hill.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height 5 meters. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are respectively 300 and 600. Find the height of the tower.
A TV tower stands vertically on a bank of a river/canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From a point 20 m away this point on the same bank, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the river/canal.
From a point on a bridge across a river, the angles of depression of the banks on opposite side of the river are 30° and 45° respectively. If the bridge is at the height of 30 m from the banks, find the width of the river.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 300. Calculate the distance of the cliff from the ship and the height of the cliff.
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
If the angle of elevation of a cloud from a point h meters above a lake is a and the angle of depression of its reflection in the lake be b, prove that the distance of the cloud from the point of observation is `(2h sec alpha)/(tan beta - tan alpha)`
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
A statue 1.46m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the status is 60 and from the same point, the angle of elevation of the top of the pedestal is 45 . Find the height of the pedestal.
The angles of elevation and depression of the top and bottom of a light-house from the top of a 60 m high building are 30° and 60° respectively. Find (i) the difference between the heights of the light-house and the building. (ii) the distance between the light-house and the building.
A storm broke a tree and the tree top rested on ground 20 m away from the
base of the tree, making an angle of 60o with the ground. Find the height
of the tree.
The angle of depression of a car, standing on the ground, from the top of a 75 m tower, is 30°. The distance of the car from the base of the tower (in metres) is
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the height of the lamp post
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the distance between the lamp post and the apartment `(sqrt(3) = 1.732)`
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between A and B. (tan 20° = 0.3640, `sqrt3` = 1.732)

At some time of the day, the length of the shadow of a tower is equal to its height. Then, the sun’s altitude at that time is ______.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite bank of the river is 60° and when he retires 40 meters away from the tree the angle of elevation becomes 30°. The breadth of the river is ______.
