Advertisements
Advertisements
Question
At some time of the day, the length of the shadow of a tower is equal to its height. Then, the sun’s altitude at that time is ______.
Options
30°
60°
90°
45°
Solution
At some time of the day, the length of the shadow of a tower is equal to its height. Then, the sun’s altitude at that time is 45°.
Explanation:
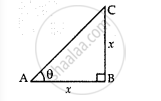
Let the height of tower BC = x m and the sun’s altitude = θ
Then Length of its shadow, AB = x m
In right-angled ΔABC, tan θ = `"BC"/"AB" = "x"/"x"` = 1
⇒ tan θ = tan 45°
θ = 45°
APPEARS IN
RELATED QUESTIONS
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/h.
An observer finds the angle of elevation of the top of the tower from a certain point on the ground as 30°. If the observe moves 20 m towards the base of the tower, the angle of elevation of the top increases by 15°, find the height of the tower.
From the top of a vertical tower, the angles depression of two cars in the same straight line with the base of the tower, at an instant are found to be 45° and 60° . If the cars are 100 m apart and are on the same side of the tower, find the height of the tower.
The angles of elevation and depression of the top and bottom of a light-house from the top of a 60 m high building are 30° and 60° respectively. Find (i) the difference between the heights of the light-house and the building. (ii) the distance between the light-house and the building.
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
In given Fig., the angle of depression from the observing position D and E of the object at A are ____________.
In given figure, AD = 4 cm, BD = 3 cm and CB = 12 cm. The value of tan `theta` is ____________.

A TV tower stands vertically on a bank of a canal, with a height of `10 sqrt3` m. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the distance between the opposite bank of the canal and the point with a 30° angle of elevation.
If one looks from a tower 10 m high at the top of a flag staff, the depression angle of 30° is made. Also, looking at the bottom of the staff from the tower, the angle of the depression made is of 60°. Find the height of the flag staff.
