Advertisements
Advertisements
प्रश्न
At some time of the day, the length of the shadow of a tower is equal to its height. Then, the sun’s altitude at that time is ______.
विकल्प
30°
60°
90°
45°
उत्तर
At some time of the day, the length of the shadow of a tower is equal to its height. Then, the sun’s altitude at that time is 45°.
Explanation:
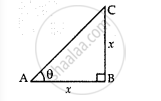
Let the height of tower BC = x m and the sun’s altitude = θ
Then Length of its shadow, AB = x m
In right-angled ΔABC, tan θ = `"BC"/"AB" = "x"/"x"` = 1
⇒ tan θ = tan 45°
θ = 45°
APPEARS IN
संबंधित प्रश्न
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be a and 3. If the height of the lighthouse be h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance
`(h(tan alpha + tan beta))/(tan alpha tan beta)` meters
The horizontal distance between two poles is 15 m. The angle of depression of the top of first pole as seen from the top of second pole is 30°. If the height of the second pole is 24 m, find the height of the first pole. Use`[sqrt3=1.732]`
In given Fig., the angle of depression from the observing position D and E of the object at A are ____________.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun ____________.
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will ____________.
The angles of elevation of the top of a tower from two points distant s and t from its foot are complementary. Then the height of the tower is ____________.
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
The top of a banquet hall has an angle of elevation of 45° from the foot of a transmission tower and the angle of elevation of the topmost point of the tower from the foot of the banquet hall is 60°. If the tower is 60 m high, find the height of the banquet hall in decimals.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then find the width of the river.