Advertisements
Advertisements
Question
A TV tower stands vertically on a bank of a river/canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From a point 20 m away this point on the same bank, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the river/canal.
Solution
Let AB be the TV tower of height hm on a bank of river/canal and D be the point on the opposite of the river/canal. An angle of elevation at the top of the tower is 60° and from a point 20 m away, an angle of elevation of the tower at the same point is 30°. Let AB = h and BC = x.
Here we have to find the height and width of the river/canal.
The corresponding figure is here
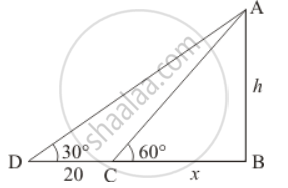
In ΔCAB
`=> tan 60^@ = ("AB")/("BC")`
`=> sqrt3 = h/x`
`=> sqrt3x = h`
`=> x = h/sqrt3`
Again in ΔDBA
`=> tan 30^@ = ("AB")/("BC")`
`=> 1/sqrt3 = h/(20 + x)`
`=> sqrt3h = 20 + x`
`=> sqrt3h = 20 + h/sqrt3`
`=> sqrt3h - h/sqrt3 = 20`
`=> (2h)/sqrt3 = 20`
`=> h = 10sqrt3`
`=> x = (10sqrt3)/sqrt3`
⇒ x = 10
Hence the height of the tower is `10sqrt3` m and width of river/canal is 10 m.
RELATED QUESTIONS
A man on a cliff observes a fishing trawler at an angle of depression of 30º which is approaching the shore to the point immediately beneath the observer with a uniform speed. 6 minutes later, the angle of depression of the trawler is found to be 60º. Caliculate the time taken by the trawler to reach the shore
Two poles of equal heights are standing opposite each other an either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30º, respectively. Find the height of poles and the distance of the point from the poles.
The angle of elevation of the top of a chimney form the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30° . If the height of the tower is 40 meters. Find the height of the chimney.
The angles of elevation and depression of the top and bottom of a light-house from the top of a 60 m high building are 30° and 60° respectively. Find (i) the difference between the heights of the light-house and the building. (ii) the distance between the light-house and the building.
If the ratio of the height of a tower and the length of its shadow is `sqrt3:1`, what is the angle of elevation of the Sun?
In given figure, AD = 4 cm, BD = 3 cm and CB = 12 cm. The value of tan `theta` is ____________.

The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
At a point on level ground, the angle of elevation of a vertical tower is, found to be α such that tan α = `1/3`. After walking 100 m towards the tower, the angle of elevation β becomes such that tan β = `3/4`. Find the height of the tower.
Two poles of heights 25 m and 35 m stand vertically on the ground. The tops of two poles are connected by a wire, which is inclined to the horizontal at an angle of 30°. Find the length of the wire and the distance between the poles.
