Advertisements
Advertisements
Question
Two poles of heights 25 m and 35 m stand vertically on the ground. The tops of two poles are connected by a wire, which is inclined to the horizontal at an angle of 30°. Find the length of the wire and the distance between the poles.
Solution
Let AC and BD are the two poles with heights of 25 m and 35 m, respectively.
Draw a horizontal line from point C to the line BD, and it meets BD at E (say).
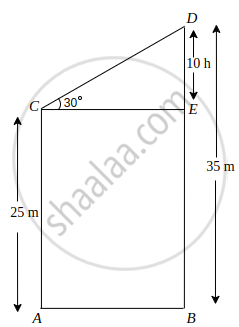
∴ DE = 35 – 25 = 10 m
In ΔCDE, tan 30° = `("DE")/("CE")`
⇒ `1/sqrt(3) = 10/("CE")`
⇒ CE = `10sqrt(3)` m
Thus, distance between the poles = BA = CE = `10sqrt(3)` m
Again, In ΔCDE, sin 30° = `("DE")/("CD")`
⇒ `1/2 = 10/("CD")`
⇒ CD = 20 m
Hence, length of the wire is 20 m.
RELATED QUESTIONS
The heights of two poles are 80 m and 62.5 m. If the line joining their tops makes an angle of 45º with the horizontal, then find the distance between the pole
Two poles of equal heights are standing opposite each other an either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30º, respectively. Find the height of poles and the distance of the point from the poles.
If a tower 30 m high, casts a shadow `10sqrt3` m long on the ground, then what is the angle of elevation of the sun?
The horizontal distance between two trees of different heights is 60 m. The angle of depression of the top of the first tree, when seen from the top of the second tree, is 45°. If the height of the second tree is 80 m, find the height of the first tree.
Two men on either side of a 75 m high building and in line with base of building observe the angles of elevation of the top of the building as 30° and 60°. Find the distance between the two men. (Use\[\sqrt{3} = 1 . 73\])
The horizontal distance between two poles is 15 m. The angle of depression of the top of first pole as seen from the top of second pole is 30°. If the height of the second pole is 24 m, find the height of the first pole. Use`[sqrt3=1.732]`
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of depression from the top of the tower to the foot of the hill is 30°. If the tower is 50 m high, find the height of the hill ?
If the angles of elevation of a tower from two points distant a and b (a>b) from its foot and in the same straight line from it are 30° and 60°, then the height of the tower is
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between B and C. (tan 20° = 0.3640, `sqrt3` = 1.732)

In given figure, the value of CE is ____________.