Advertisements
Advertisements
प्रश्न
A TV tower stands vertically on a bank of a river/canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From a point 20 m away this point on the same bank, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the river/canal.
उत्तर
Let AB be the TV tower of height hm on a bank of river/canal and D be the point on the opposite of the river/canal. An angle of elevation at the top of the tower is 60° and from a point 20 m away, an angle of elevation of the tower at the same point is 30°. Let AB = h and BC = x.
Here we have to find the height and width of the river/canal.
The corresponding figure is here
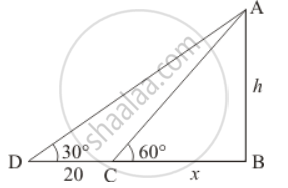
In ΔCAB
`=> tan 60^@ = ("AB")/("BC")`
`=> sqrt3 = h/x`
`=> sqrt3x = h`
`=> x = h/sqrt3`
Again in ΔDBA
`=> tan 30^@ = ("AB")/("BC")`
`=> 1/sqrt3 = h/(20 + x)`
`=> sqrt3h = 20 + x`
`=> sqrt3h = 20 + h/sqrt3`
`=> sqrt3h - h/sqrt3 = 20`
`=> (2h)/sqrt3 = 20`
`=> h = 10sqrt3`
`=> x = (10sqrt3)/sqrt3`
⇒ x = 10
Hence the height of the tower is `10sqrt3` m and width of river/canal is 10 m.
संबंधित प्रश्न
A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground, making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is sanding on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
A man on the deck of a ship, 16m above water level, observe that that angle of elevation and depression respectively of the top and bottom of a cliff are 60° and 30° . Calculate the distance of the cliff from the ship and height of the cliff.
The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30°. The distance of the car from the base of the tower (in m.) is:
If the angles of elevation of a tower from two points distant a and b (a>b) from its foot and in the same straight line from it are 30° and 60°, then the height of the tower is
In given figure, the value of ZC is ____________.
A Technician has to repair light on a pole of height 10 m. She needs to reach a point 1 m below the top of the pole to undertake the repair work. What should be the length of the ladder that she should use which, when inclined at an angle of 60∘ to the ground, would enable her to reach the required position? Also, how far from the foot of the pole should she place the foot of the ladder?
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top remains unchanged.
