Advertisements
Advertisements
प्रश्न
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is sanding on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
उत्तर
Let AB be the string of string x m. let DF be the ground and a boy flying the kite of 100 m string at an elevation of 30 °. And another boy flying the kite of 10 m high building at an angle of elevation of 45°.
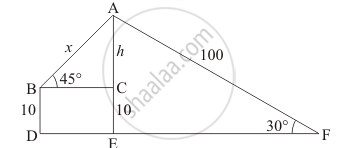
Let AE = H, AC = h, CE = 10, AB = x and AF = 100 m
∠ABC = 45°, ∠AFE = 30°
Here we have to find length of string.
We use trigonometric ratios.
`In ΔAFE`
`=> sin 30^@ = (AE)/(AF)`
`=> 1/2 = H/100`
=> h = 50
=> h = H - 10
=> h = 50 - 10
=> h = 40
Again in ΔABC
`=> sin 45^@ = (AB)/(AC)`
`=> 1/sqrt2 = h/x`
`=> 1/sqrt2 = 40/x`
`=> x = 40sqrt2`
Hence the leght of string is `40sqrt2`
APPEARS IN
संबंधित प्रश्न
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
The angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation of the top is 45°. Calculate the height of the tower.
From the top of a tower of height 50 m, the angles of depression of the top and bottom of a pole are 30° and 45° respectively. Find
(i) how far the pole is from the bottom of a tower,
(ii) the height of the pole. (Use \[\sqrt{3} = 1 . 732\])
A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is
The ratio of the length of a rod and its shadow is `1 : sqrt3`. The angle of elevation of the sum is
In given figure, the length of AP is ____________.

Two vertical poles of different heights are standing 20m away from each other on the level ground. The angle of elevation of the top of the first pole from the foot of the second pole is 60° and angle of elevation of the top of the second pole from the foot of the first pole is 30°. Find the difference between the heights of two poles. (Take `sqrt(3)` = 1.73)
If one looks from a tower 10 m high at the top of a flag staff, the depression angle of 30° is made. Also, looking at the bottom of the staff from the tower, the angle of the depression made is of 60°. Find the height of the flag staff.
Let AB and PQ be two vertical poles, 160 m apart from each other. Let C be the middle point of B and Q, which are feet of these two poles. Let `π/8` and θ be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then, tan2 θ is equal to ______.
A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high tower observes two cars at angles of depression of 30° and 60°, which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars. (use `sqrt(3)` = 1.73)
