English Medium
Academic Year: 2023-2024
Date & Time: 11th March 2024, 10:30 am
Duration: 3h
Advertisements
General Instructions:
Read the following instructions carefully and follow them:
- This question paper contains 38 questions. All questions are compulsory.
- Question paper is divided into Five Sections − Section A, B, C, D and E.
- In Section A, question number 1 to 18 are Multiple choice questions (MCQs) and question number 19 and 20 are Assertion − Reason based questions of 1 mark each.
- In Section B, question number 21 to 25 are Very short answer (VSA) type questions of 2 marks each.
- In Section C, question number 26 to 31 are Short answer (SA) type questions carrying 3 marks each.
- In Section D, question number 32 to 35 are Long answer (LA) type questions carrying 5 marks each.
- In Section – E question number 36 to 38 are Case Study based questions
carrying 4 marks each. Internal choice is provided in 2 marks question
in each case-study. - There is no overall choice. However, an internal choice has been provided in 2 questions in Section B, 2 questions in Section C, 2 questions in Section D and 3 questions in Section E.
- Draw neat figures wherever required. Take `pi = 22/7` wherever required if not stated.
- Use of calculators is not allowed.
The difference of the areas of a minor sector of angle 120° and its corresponding major sector of a circle of radius 21 cm is ______.
231 cm2
462 cm2
346.5 cm2
693 cm2
Chapter:
The annual rainfall record of a city for 66 days is given in the following table:
| Rainfall (in cm): | 0 − 10 | 10 − 20 | 20 − 30 | 30 − 40 | 40 − 50 | 50 − 60 |
| Number of days : | 22 | 10 | 8 | 15 | 5 | 6 |
The difference of upper limits of modal and median classes is ______.
10
15
20
30
Chapter:
In the given figure, tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80°. ∠ABO is equal to ______.
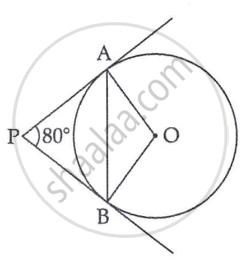
40°
80°
100°
50°
Chapter:
`(1 + tan^2 "A")/(1 + cot^2 "A")` is equal to ______.
sec2 A
- 1
cot2 A
tan2 A
Chapter: [0.051] Introduction to Trigonometry
If sin2θ = `3/4`, then θ is ______.
30°
45°
60°
90°
Chapter:
The zeroes of the polynomial 3x2 − 5x − 2, are ______.
`1/3, 2`
`(-1)/3, 2`
`(-1)/3, -2`
`1/3, -2`
Chapter:
A pole `7 sqrt3` m high casts a shadow 21 m long on the ground, then the sun's elevation is ______.
30°
45°
60°
90°
Chapter:
The HCF of the smallest 2-digit number and the smallest composite number is ______.
4
20
2
10
40
Chapter: [0.011000000000000001] Real Numbers
The total surface area of a solid hemisphere of radius 7 cm is ______.
447π cm2
239 π cm2
174 π cm2
147 π cm2
98 π cm2
196 π cm2
`228 2/3 π "cm"^2`
Chapter: [0.062] Surface Areas and Volumes
If sin A = `3/5`, then value of cot A is ______.
`3/4`
`4/3`
`4/5`
`5/4`
Chapter:
The graph of a pair of linear equations a1x + b1y = c1, and a2x + b2Y = c2 in two variables x and y represents parallel lines, if ______.
`a_1/a_2 ≠ b_1/b_2`
`a_1/a_2 = b_1/b_2 = c_1/c_2`
`a_1/a_2 ≠ b_1/b_2 = c_1/c_2`
`a_1/a_2 = b_1/b_2 ≠ c_1/c_2`
Chapter:
A line intersecting a circle in two distinct points is called a ______.
secant
chord
diameter
tangent
Chapter:
The value of 'k' for which the pair of linear equations x + y − 4 = 0 and 2x + ky − 8 = 0 has infinitely many solutions is ______.
k ≠ 2
k ≠ −2
k = 2
k = −2
Chapter:
A quadratic polynomial, the sum of whose zeroes is −5 and their product is 6, is ______.
x2 + 5x + 6
x2 − 5x + 6
x2 − 5x − 6
− x2 + 5x + 6
Chapter:
If P(A) denotes the probability of an event A, then ______.
P(A) < 0
P(A) > 1
0 ≤ P(A) ≤ 1
–1 ≤ P(A) ≤ 1
Chapter: [0.07200000000000001] Probability
Which of the following quadratic equations has −1 as a root?
x2 − 4x − 5 = 0
−x2 − 4x + 5 = 0
x2 + 3x + 4 = 0
x2 − 5x + 6 = 0
Chapter:
The distance of the point (3, 4) from the origin is ______.
25
5
7
1
−5
Chapter:
Advertisements
If the first term of an AP is − 3 and common difference − 2, then the seventh term is ______.
−9
9
−17
−15
Chapter:
Assertion (A): The point (0, 4) lies on y-axis.
Reason (R): The x-coordinate of a point on y-axis is zero.
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
Assertions (A) is true but reason (R) is false.
Assertions (A) is false but reason (R) is true.
Chapter: [0.031] Lines (In Two-dimensions) [0.031] Lines (In Two-dimensions)
Assertion (A): A line drawn parallel to any one side of a triangle intersects the other two sides in the same ratio.
Reason (R): Parallel lines cannot be drawn to any side of a triangle.
Both Assertion (A) and Reason (R) are correct and Reason (R) is the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are correct but Reason (R) is not the correct explanation of Assertion (A).
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Chapter:
In the given figure, OA·OB = OC·OD, Prove that ΔAOD ∼ ΔCOB.
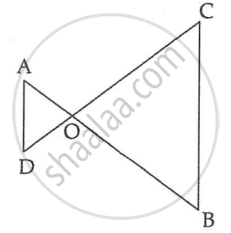
Chapter:
In the given figure, ∠D = ∠E and `"AD"/"DB" = "AE"/"EC"` Prove that ΔABC is isosceles.

Chapter:
A lot consists of 165 ball pens, of which 30 are defective and the others are good. Rakshita will buy a pen if it is good. The shopkeeper draws one pen at random and gives it to Rakshita. What is the probability that she will buy it?
Chapter:
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Chapter: [0.042] Circles
Find the HCF of 84 and 144 by prime factorisation method.
Chapter:
The sum of two natural numbers is 70 and their difference is 10. Find the natural numbers.
Chapter:
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships warned. [Use π = 3.14]
Chapter: [0.061] Areas Related to Circles
Zeroes of the quadratic polynomial x2 + x − 6 are 'α' and 'β'. Construct a quadratic polynomial whose zeroes are `1/α "and" 1/β`.
Chapter:
Find the zeros of the polynomial 2x2 + 3x − 2 and verify the relationship between the zeroes and the coefficients.
Chapter:
Prove that `tan θ/(1 - cot θ) + cot θ/(1 - tanθ)` = 1 + sec θ cosec θ
Chapter: [0.051] Introduction to Trigonometry
Advertisements
Two dice are tossed simultaneously. Find the probability of getting an even number on both the dice.
Chapter:
A car has two wipers that do not overlap. Each wiper has a blade of length 21 cm sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades. `("Take" π =22/7)`
Chapter: [0.061] Areas Related to Circles
In two concentric circles, a chord of length 24 cm of larger circle touches the smaller circle, whose radius is 5 cm. Find the radius of the larger circle.
Chapter:
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
Chapter: [0.042] Circles
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
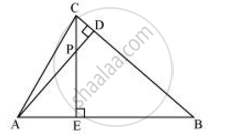
ΔAEP ∼ ΔCDP
Chapter: [0.040999999999999995] Triangles
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔABD ∼ ΔCBE
Chapter: [0.040999999999999995] Triangles
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
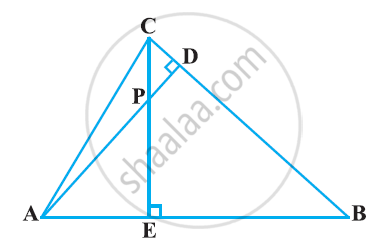
ΔAEP ∼ ΔADB
Chapter: [0.040999999999999995] Triangles
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
Chapter: [0.040999999999999995] Triangles
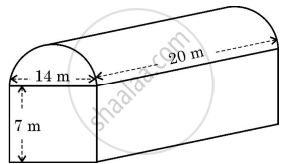
A textile industry runs in a shed. This shed is in the shape of a cuboid surmounted by a half-cylinder. If the base of the industry is of dimensions 14 m × 20 m and the height of the cuboidal portion is 7 m, find the volume of air that the industry can hold. Further, suppose the machinery in the industry occupies a total space of 400 m3. Then, how much space is left in the industry?
Chapter:
From a solid cylinder of height 8 cm and radius 6 cm, a conical cavity of the same height and same radius is carved out. Find the total surface area of the remaining solid. (Take π = 3.14)
Chapter:
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Chapter: [0.053] Some Applications of Trigonometry
A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was Rs 90, find the number of articles produced and the cost of each article.
Chapter: [0.023] Quadratic Equations
Heart Rate : The heart rate is one of the 'vital signs' of health in the human body. It measures the number of times per minute that the heart contracts or beats. While a normal heart rate does not guarantee that a person is free of health problems, it is a useful benchmark for identifying a range of health issues.
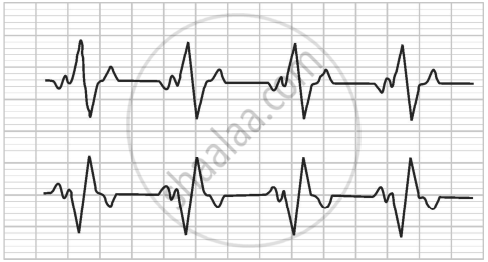
Thirty women were examined by doctors of AIIMS and the number of heart beats per minute were recorded and summarized as follows:
| Number of heart beats per minute | Number of Women |
| 65 − 68 | 2 |
| 68 − 71 | 4 |
| 71 − 74 | 3 |
| 74 − 77 | 8 |
| 77 − 80 | 7 |
| 80 − 83 | 4 |
| 83 − 86 | 2 |
Based on the above information, answer the following questions:
- How many women are having heart beat in the range 68 − 77? (1)
- What is the median class of heart beats per minute for these women? (1)
-
- Find the modal value of heart beats per minute for these women. (2)
OR - Find the median value of heart beats per minute for these women. (2)
- Find the modal value of heart beats per minute for these women. (2)
Chapter:
The top of a table is hexagonal in shape.
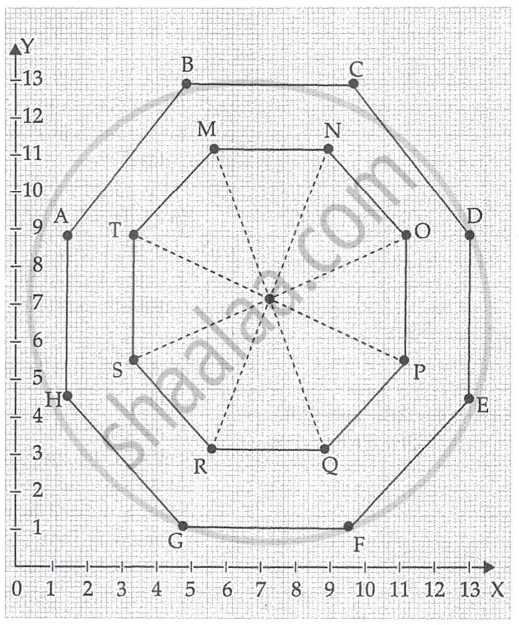
On the basis of the information given above, answer the following questions:
- Write the coordinates of A and B. (1)
- Write the coordinates of the mid-point of the line segment joining C and D. (1)
-
- Find the distance between M and Q. (2)
OR - Find the coordinates of the point which divides the line segment joining M and N in the ratio 1:3 internally. (2)
- Find the distance between M and Q. (2)
Chapter:
|
Saving money is a good habit and it should be inculcated in children right from the beginning. Rehan's mother brought a piggy bank for Rehan and put one ₹ 5 coin of her savings in the piggy bank on the first day. She increases his savings by one ₹ 5 coin daily.
|
Based on the above information, answer the following questions:
- How many coins were added to the piggy bank on 8th day? (1)
- How much money will be there in the piggy bank after 8 days? (1)
-
- If the piggy bank can hold one hundred twenty ₹ 5 coins in all, find the number of days she can contribute to put ₹ 5 coins into it. (2)
OR - Find the total money saved when the piggy bank is full. (2)
- If the piggy bank can hold one hundred twenty ₹ 5 coins in all, find the number of days she can contribute to put ₹ 5 coins into it. (2)
Chapter:
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CBSE previous year question papers Class 10 Mathematics with solutions 2023 - 2024
Previous year Question paper for CBSE Class 10 Maths-2024 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CBSE Class 10.
How CBSE Class 10 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.

