Question

The top of a table is hexagonal in shape.

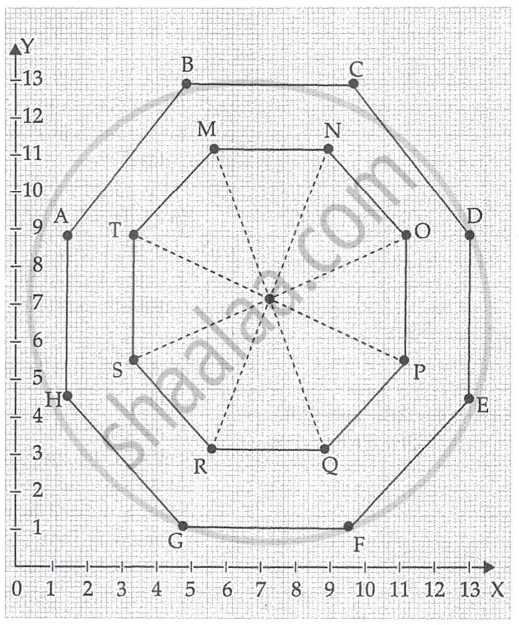
On the basis of the information given above, answer the following questions:

1. Write the coordinates of A and B. (1)
2. Write the coordinates of the mid-point of the line segment joining C and D. (1)
3. 1. Find the distance between M and Q. (2)
      OR
   2. Find the coordinates of the point which divides the line segment joining M and N in the ratio 1:3 internally. (2)

Answer 1

As per given figure

(i) Co-ordinates of A = (1, 9)

Co-ordinates of B = (5, 13)

(ii) Mid-point ofline segment = `((x_1 + x_2)/2,  (y_1 + y_2)/2)`

Coordinates of C = (9, 13)

Coordinates of D = (13, 9)

Thus, mid point = `[((9 + 13)/2)((13 + 9)/2)]`

= `(22/2, 22/2)`

= (11,11)

(iii) (a) Distance between two points

= `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)`

Here Coordinates of M (5, 11)

Coordinates of Q (9, 3)

Distance between M and Q

d = `sqrt((9 - 5)^2 + (3 - 11)^2)`

= `sqrt((4)^2 + (-8)^2)`

= `sqrt(16 + 64)`

= `sqrt 80`

= `4sqrt5`

OR

(iii) (b) Coordinates of point which divides the line segment joining M and N in the ratio 1 : 3 internally.

`"x" = (("mx"_2 + "nx"_1)/("m" + "n")),  "y" = (("my"_2 + "ny"_1)/("m" + "n"))`

Co-ordinates of M = (5, 11)

Coordinates of N = (9, 11)

`"x" = ((1 xx 9 + 3 xx 5)/(1 + 3))`

= `(9 + 15)/4`

= `24/4`

= 6

`"y" = ((1 xx 11 + 3 xx 11)/(1 + 3))`

= `((11 + 33)/4)`

= `44/4`

= 11

Thus Coordinates of point = (6, 11)