Advertisements
Advertisements
Question
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.

Solution 1
In ΔABC,
`("AB")/("BC")` = tan 60°
`("AB")/("BC") = sqrt3`
`"BC" = ("AB")/sqrt3`
In ΔABD,
`("AB")/("BD") `= tan 30°
`("AB")/("BC"+"CD") = 1/sqrt3`
`("AB")/(("AB")/sqrt3+20) = 1/sqrt3`
`("AB"sqrt3)/("AB"+20sqrt3) = 1/sqrt3`
`3"AB" = "AB"+20sqrt3`
`2"AB" = 20sqrt3`
`"AB" = 10sqrt3 m`
`"BC" = ("AB")/sqrt3`
= `((10sqrt3)/sqrt3)m`
= 10 m
Therefore, the height of the tower is `10sqrt3` m and the width of the canal is 10 m.
Solution 2
Let PQ = h m be the height of the TV tower and BQ = x m be the width of the canal.
We have,
AB = 20 m, ∠PAQ = 30°, ∠BQ = x and PQ = h
In ΔPBQ,
`tan 60° = ("PQ")/("BQ")`
⇒ `sqrt(3) = h/x`
⇒ `h = x sqrt(3) ` ...(1)
Again in ΔAPQ,
`tan 30° = ("PQ")/("AQ")`
⇒ `1/sqrt(3) = h/("AB" +"BQ")`
⇒ `1/sqrt(3) = (x sqrt(3))/(20+3)` ...[Using (1)]
⇒ 3x = 20 + x
⇒ 3x - x = 20
⇒ 2x = 20
⇒ x = `20/2`
⇒ x = 10 m
Substituting x = 10 in (i), we get
h = `10 sqrt(3)` m
So, the height of the TV tower is 10`sqrt(3)` m and the width of the canal is 10 m.
RELATED QUESTIONS
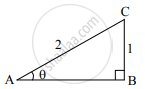
In the following figure, in ΔABC, BC = 1, AC = 2, ∠B = 90°. Find the value of sin θ.
The angles of depression of the top and bottom of a 50 m high building from the top of a tower are 45° and 60° respectively. Find the height of the tower and the horizontal distance between the tower and the building (use `sqrt3`=1.73)
A kit is flying at a height of 75 metres from the ground level, attached to a string inclined at 60 to the horizontal. Find the length of the string to the nearest metre.
From the top of a 15 m high building, the angle of elevation of the top of a tower is found to be 30°. From the bottom of the same building, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower and the distance between tower and the building.
On a horizontal plane, there is a vertical tower with a flagpole on the top of the tower. At a point 9 meters away from the foot of the tower the angle of elevation of the top and bottom of the flagpole are 60° and 30° respectively. Find the height of the tower and the flagpole mounted on it.
The horizontal distance between two trees of different heights is 60 m. The angle of depression of the top of the first tree, when seen from the top of the second tree, is 45°. If the height of the second tree is 80 m, find the height of the first tree.
The angles of elevation of the top of a rock from the top and foot of a 100 m high tower are respectively 30° and 45°. Find the height of the rock.
A boy standing at a distance of 48 meters from a building observes the top of the building and makes an angle of elevation of 30°. Find the height of the building.
AB is a pole of height 6 m standing at a point B and CD is a ladder inclined at angle of 600 to the horizontal and reaches upto a point D of pole . If AD = 2.54 m , find the length of the ladder.
A ladder makes an angle of 60º with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is
If two circles having centers P and Q and radii 3 cm and 5 cm. touch each other externally, find the distance PQ.
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60ϒ and from the same point the angle of elevation of the top of the pedestal is 40ϒ. Find the height of the pedestal. (tan 40° = 0.8391, `sqrt(3)` = 1.732)
A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is `30sqrt(3)` feet from the entrance of the lift, find the speed of the lift which is descending.
The angles of elevation of the top of the rock from the top and foot of 100 m high tower are respectively 30° and 45°. The height of the rock is ____________.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
Two towers A and B are standing some distance apart. From the top of tower A, the angle of depression of the foot of tower B is found to be 30°. From the top of tower B, the angle of depression of the foot of tower A is found to be 60°. If the height of tower B is ‘h’ m then the height of tower A in terms of ‘h’ is ____________ m.
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.
In the given figure, AB is tower of height 50 m. A man standing on its top, observes two car on the opposite sides of the tower with angles of depression 30° and 45° respectively. Find the distance between the two cars.

From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, find the width of the river. (Use `sqrt(3)` = 1.73)
