Advertisements
Advertisements
Question
From the top of a 15 m high building, the angle of elevation of the top of a tower is found to be 30°. From the bottom of the same building, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower and the distance between tower and the building.
Solution
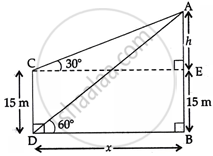
Let AB = tower
CD = building
Such that ∠ACE = 30°
∠ADB = 60°
AE = h m (say)
EB = CD = 15 m
and BD = x m (say)
= CE
Now, In ΔAEC, ∠E = 90° we have
`tan 30"°" = h/x`
⇒ `1/sqrt3 = h/x`
⇒ x = `sqrt3 * h` ...(i)
Again in ΔABD, ∠B = 90° we have
`tan 60"°" = (AB)/(BD)`
⇒ `sqrt3 = (h + 15)/x`
⇒ `sqrt3 * (sqrt3 * h) = h + 15` ...[∵ from (i) x = `sqrt3 .` h]
⇒ 3h − h = 15
⇒ h = 7.5 m
⇒ x = `sqrt3h = sqrt3 xx 7.5 ≈ 1.732 xx 7.5` m
x ≈ 12.99 m
Hence height of the tower = 7.5 + 15 = 22.5 m
and distance between tower and building = 12.99 m
RELATED QUESTIONS
If the angle of elevation of a cloud from a point h metres above a lake is α and the angle of depression of its reflection in the lake is β, prove that the height of the cloud is
`\frac{h(\tan\alpha +\tan \beta )}{\tan \beta -\tan \alpha }`
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between the points.
An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and 60° respectively. Find the width of the river. [Use `sqrt3` = 1⋅732]
A tower stands vertically on the ground. From a point on the ground 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 60°. What is the height of the tower?
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
A kite is flying at a height of 45 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is
60°. Find the length of the string assuming that there is no slack in the string.
A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of same base radius. Find the length of the canvas used in making the tent, if the breadth of the canvas is 1.5 m.
The length of the shadow of a tower standing on level ground is found to be 2x metres longer when the sun's elevation is 30°than when it was 45°. The height of the tower in metres is
Two vertical poles of different heights are standing 20m away from each other on the level ground. The angle of elevation of the top of the first pole from the foot of the second pole is 60° and angle of elevation of the top of the second pole from the foot of the first pole is 30°. Find the difference between the heights of two poles. (Take `sqrt(3)` = 1.73)
