English Medium
Academic Year: 2023-2024
Date & Time: 11th March 2024, 10:30 am
Duration: 3h
Advertisements
General Instructions:
Read the following instructions carefully and follow them:
- This question paper contains 38 questions. All questions are compulsory.
- This question paper is divided into five Sections - A, B, C, D and E.
- In Section A, Question numbers 1 to 18 are multiple choice questions (MCQs) and question numbers 19 and 20 are Assertion - Reason based questions of 1 mark each.
- In Section B, Question numbers 21 to 25 are very short answer (VSA) type questions, carrying 2 marks each.
- In Section C, Question numbers 26 to 31 are short answer (SA) type questions, carrying 3 marks each.
- In Section D, Question numbers 32 to 35 are long answer (LA) type questions carrying 5 marks each.
- In Section E, Question numbers 36 to 38 are case-study based integrated questions carrying 4 marks each. Internal choice is provided in 2 marks question in each case-study.
- There is no overall choice. However, an internal choice has been provided in 2 questions in Section B, 2 questions in Section C, 2 questions in Section D and 3 questions of 2 marks in Section E.
- Draw neat diagrams wherever required. Take `π=22/7` wherever required, if not stated.
- Use of calculators is NOT allowed.
If two positive integers p and q can be expressed as p = 18 a2b4 and q = 20 a3b2, where a and b are prime numbers, then LCM (p, q) is ______.
2 a2b2
180 a2b2
12 a2b2
180 a3b4
Chapter:
In an A.P., if the first term (a) = −16 and the common difference (d) = −2, then the sum of first 10 terms is ______.
−200
−70
−250
250
Chapter:
For some data x1, x2, ..... xn with respective frequencies f1, f2, .... fn, the value of `sum_1^nf_i(x_i - barx)` is equal to ______.
`nbarx`
1
`sumf_i`
0
Chapter:
The volume of the largest right circular cone that can be carved out from a solid cube of edge 2 cm is ______.
`(4pi)/3` cu cm
`(5pi)/3` cu cm
`(8pi)/3` cu cm
`(2pi)/3` cu cm
Chapter:
A solid sphere is cut into two hemispheres. The ratio of the surface areas of sphere to that of two hemispheres taken together, is ______.
1 : 1
1 : 4
2 : 3
3 : 2
Chapter:
The centre of a circle is at (2, 0). If one end of a diameter is at (6, 0), then the other end is at ______.
(0, 0)
(4, 0)
(−2, 0)
(−6, 0)
Chapter:
One card is drawn at random from a well shuffled deck of 52 playing cards. The probability that it is a red ace card, is ______.
`1/13`
`1/26`
`1/52`
`1/2`
Chapter:
The middle most observation of every data arranged in order is called ______.
mode
median
mean
deviation
Chapter:
For θ = 30°, the value of (2 sin θ cos θ) is ______.
1
`sqrt3/2`
`sqrt3/4`
`3/2`
Chapter:
If the roots of equation ax2 + bx + c = 0, a ≠ 0 are real and equal, then which of the following relation is true?
`a = b^2/c`
b2 = ac
`ac = b^2/4`
`c = b^2/a`
Chapter:
From the data 1, 4, 7, 9, 16, 21, 25, if all the even numbers are removed, then the probability of getting at random a prime number from the remaining is ______.
`2/5`
`1/5`
`1/7`
`2/7`
Chapter:
AD is a median of ΔABC with vertices A (5, -6), B (6, 4) and C (0, 0). Length AD is equal to ______.
`sqrt68` units
`2sqrt15` units
`sqrt101` units
10 units
Chapter:
Two dice are rolled together. The probability of getting sum of numbers on the two dice as 2, 3 or 5, is ______.
`7/36`
`11/36`
`5/36`
`4/9`
Chapter:
If the distance between the points (3, −5) and (x, −5) is 15 units, then the values of x are ______.
12, −18
−12, 18
18, 5
−9, −12
Chapter:
In the given figure, graphs of two linear equations are shown. The pair of these linear equations is ______.
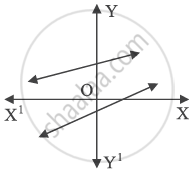
consistent with unique solution.
consistent with infinitely many solutions.
inconsistent.
inconsistent but can be made consistent by extending these lines.
Chapter:
If α, β are the zeroes of the polynomial 6x2 − 5x − 4, then `1/alpha + 1/beta` is equal to ______.
`5/4`
`-5/4`
`4/5`
`5/24`
Chapter:
Advertisements
If sec θ - tan θ = m, then the value of sec θ + tan θ is ______.
`1 - 1/m`
`m^2 - 1`
`1/m`
-m
Chapter:
The zeroes of a polynomial x2 + px + q are twice the zeroes of the polynomial 4x2 - 5x - 6. The value of p is ______.
`-5/2`
`5/2`
-5
10
Chapter:
Assertion (A): The tangents drawn at the end points of a diameter of a circle, are parallel.
Reason (R): Diameter of a circle is the longest chord.
Both, Assertion (A) and Reason (R) are true and Reason (R) is correct explanation of Assertion (A).
Both, Assertion (A) and Reason (R) are true but Reason (R) is not correct explanation for Assertion (A).
Assertion (A) is true but Reason (R) is false.
Assertion (A) is false but Reason (R) is true.
Chapter:
Assertion (A): If the graph of a polynomial touches x-axis at only one point, then the polynomial cannot be a quadratic polynomial.
Reason (R): A polynomial of degree n(n >1) can have at most n zeroes.
Both, Assertion (A) and Reason (R) are true and Reason (R) is correct explanation of Assertion (A).
Both, Assertion (A) and Reason (R) are true but Reason (R) is not correct explanation for Assertion (A).
Assertion (A) is true but Reason (R) is false.
Assertion (A) is false but Reason (R) is true.
Chapter:
In a pack of 52 playing cards one card is lost. From the remaining cards, a card is drawn at random. Find the probability that the drawn card is queen of heart, if the lost card is a black card.
Chapter:
Evaluate:
`2 sqrt2 cos 45^circ sin 30^circ + 2 sqrt3 cos 30^circ`
Chapter:
If A = 60° and B = 30°, verify that: sin (A + B) = sin A cos B + cos A sin B.
Chapter:
Prove that `5 - 2sqrt3` is an irrational number. It is given that `sqrt3` is an irrational number.
Chapter:
Show that the number 5 × 11 × 17 + 3 × 11 is a composite number.
Chapter:
Solve the following system of linear equations algebraically:
2x + 5y = −4; 4x − 3y = 5
Chapter:
In ΔABC, altitudes AD and BE are drawn. If AD = 7 cm, BE = 9 cm and EC = 12 cm then, find the length of CD.
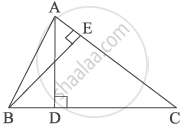
Chapter:
The sum of the digits of a 2-digit number is 14. The number obtained by interchanging its digits exceeds the given number by 18. Find the number.
Chapter:
The inner and outer radii of a hollow cylinder surmounted on a hollow hemisphere of same radii are 3 cm and 4 cm respectively. If height of the cylinder is 14 cm, then find its total surface area (inner and outer).
Chapter:
In a teachers' workshop, the number of teachers teaching French, Hindi and English are 48, 80 and 144 respectively. Find the minimum number of rooms required if in each room the same number of teachers are seated and all of them are of the same subject.
Chapter:
Advertisements
In the given figure, AB is a diameter of the circle with centre O. AQ, BP and PQ are tangents to the circle. Prove that ∠POQ = 90°.
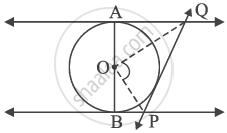
Chapter:
A circle with centre O and radius 8 cm is inscribed in a quadrilateral ABCD in which P, Q, R, S are the points of contact as shown. If AD is perpendicular to DC, BC = 30 cm and BS = 24 cm, then find the length DC.
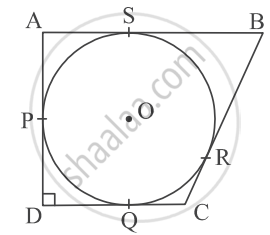
Chapter:
Find the ratio in which the point `(8/5, y)` divides the line segment joining the points (1, 2) and (2, 3). Also, find the value of y.
Chapter:
ABCD is a rectangle formed by the points A (−1,−1), B (−1, 6), C (3, 6) and D (3, −1). P, Q, R and S are midpoints of sides AB, BC, CD and DA respectively. Show that diagonals of the quadrilateral PQRS bisect each other.
Chapter:
Prove that:
`tan theta/(1 - cot theta) + cot theta/(1 - tan theta)` = 1 + sec θ cosec θ
Chapter:
From the top of a 15 m high building, the angle of elevation of the top of a tower is found to be 30°. From the bottom of the same building, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower and the distance between tower and the building.
Chapter: [0.053] Some Applications of Trigonometry
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
Chapter: [0.040999999999999995] Triangles [0.040999999999999995] Triangles [0.040999999999999995] Triangles
In the given figure PA, QB and RC are each perpendicular to AC. If AP = x, BQ = y and CR = z, then prove that `1/x + 1/z = 1/y`
Chapter:
The sum of first and eighth terms of an A.P. is 32 and their product is 60. Find the first term and common difference of the A.P. Hence, also find the sum of its first 20 terms.
Chapter:
In an A.P. of 40 terms, the sum of first 9 terms is 153 and the sum of last 6 terms is 687. Determine the first term and common difference of A.P. Also, find the sum of all the terms of the AP.
Chapter:
In the given figure, diameters AC and BD of the circle intersect at O. If ∠AOB = 60° and OA = 10 cm, then:
- find the length of the chord AB.
- find the area of shaded region.
(Take π = 3.14 and `sqrt3 = 1.73`)
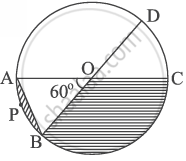
Chapter:
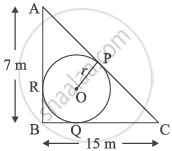
|
A backyard is in the shape of a triangle ABC with right angle at B. AB = 7m and BC = 15 m. A circular pit was dug inside it such that it touches the walls AC, BC and AB at P, Q and R respectively such that AP = x m.
|
Based on the above information, answer the following questions:
- Find the length of AR in terms of x. [1]
- Write the type of quadrilateral BQOR. [1]
-
- Find the length PC in terms of x and hence find the value of x. [2]
OR - Find x and hence find the radius r of circle. [2]
- Find the length PC in terms of x and hence find the value of x. [2]
Chapter:
| A rectangular floor area can be completely tiled with 200 square tiles. If the side length of each tile is increased by 1 unit, it would take only 128 tiles to cover the floor. |
- Assuming the original length of each side of a tile be x units, make a quadratic equation from the above information. [1]
- Write the corresponding quadratic equation in standard form. [1]
-
- Find the value of x, the length of side of a tile by factorisation. [2]
OR - Solve the quadratic equation for x, using quadratic formula. [2]
- Find the value of x, the length of side of a tile by factorisation. [2]
Chapter:
|
BINGO is game of chance. The host has 75 balls numbered 1 through 75. Each player has a BINGO card with some numbers written on it. The participant cancels the number on the card when called out a number written on the ball selected at random. Whosoever cancels all the numbers on his/her card, says BINGO and wins the game.
The table given below, shows the data of one such game where 48 balls were used before Tara said 'BINGO'.
|
Based on the above information, answer the following:
- Write the median class. [1]
- When first ball was picked up, what was the probability of calling out an even number? [1]
-
- Find median of the given data. [2]
OR - Find mode of the given data. [2]
- Find median of the given data. [2]
Chapter:
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CBSE previous year question papers Class 10 Mathematics with solutions 2023 - 2024
Previous year Question paper for CBSE Class 10 Maths-2024 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CBSE Class 10.
How CBSE Class 10 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.