Question

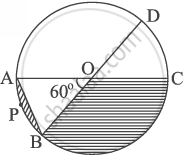
In the given figure, diameters AC and BD of the circle intersect at O. If ∠AOB = 60° and OA = 10 cm, then:

1. find the length of the chord AB.
2. find the area of shaded region.
   (Take π = 3.14 and `sqrt3 = 1.73`)

Answer 1

Given, OA = 10 cm

AC & BD are diameters that intersect at O

Hence, O is the center

⇒ OA = OB = OC = 10 cm

and ∠AOB = 60°

⇒ ∠ABO = ∠BAO = `(120^circ)/2 = 60^circ`      ...[∵ OA = OB ⇒ ∠OAB = ∠OBA]

Hence, ΔOAB = equilateral triangle

i. So AB = OA = OB = 10 cm     ...(Sides of equilateral triangle)

ii. Area of shaded region = sector area (OBPC) + [Sector area OAQB − area of ΔOAB]

= `[(120^circ)/(360^circ) xx pi xx 10^2 + (60^circ)/(360^circ) xx pi xx 10^2 - sqrt3/4 xx 10^2]` cm²

= `((180^circ)/(360^circ) xx pi xx 100 - sqrt3/4 xx 100)` cm²

= `(50pi - sqrt3/4 xx 100)` cm²

= (50 × 3.14 − 1.73 × 25) cm²

= 157 cm² − 43.25 cm²

= 113.75 cm²

Hence, Required shaded area = 113.75 cm²