Advertisements
Advertisements
Question
In the given figure, AB is a diameter of the circle with centre O. AQ, BP and PQ are tangents to the circle. Prove that ∠POQ = 90°.
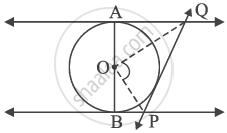
Sum
Solution
In the given figure, join OR.
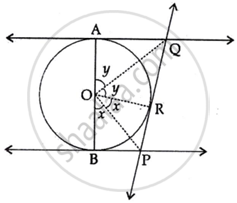
In ΔOBP and ΔORP,
PB = PR ...(Tangents drawn from outside point P)
OB = OR ...(Radii of the circle)
OP = OP ...(Common side)
∴ ΔOBP ≅ ΔORP ...(By SSS)
Therefore, ∠BOP = ∠POR = x ...(cpct)
In ΔOAQ and ΔORQ,
QA = QR ...(Tangents drawn from outside point Q)
OA = OR ...(Radii of the circle)
OQ = OQ ...(common side)
∴ ΔOAQ ≅ ΔORQ ...(By SSS)
Therefore, ∠AOQ = ∠ROQ = y ...(cpct)
As, AOB is a straight line, given
So, ∠AOB = 180°
∴ x + x + y + y = 180°
⇒ 2(x + y ) = 180°
⇒ x + y = 90°
⇒ ∠POQ = 90°
Hence Proved
shaalaa.com
Is there an error in this question or solution?
