Question

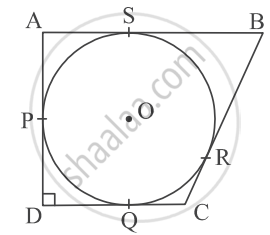
A circle with centre O and radius 8 cm is inscribed in a quadrilateral ABCD in which P, Q, R, S are the points of contact as shown. If AD is perpendicular to DC, BC = 30 cm and BS = 24 cm, then find the length DC.

Answer 1

Given BC = 30 cm, BS = 24 cm

and AD ⊥ DC

∴ ∠ADC = 90°

We know that tangents to a circle from an external point are equal in length.

∴ AS = AP

BS = BR

CR = CQ

and DP = DQ

We have, OP = OQ = OR = OS = 8 cm     ...(radii of circle)

Also, BC = BR + RC

BC = BS + RC

∴ RC = BC − BS

= 30 − 24 = 6cm

⇒ QC = 6cm      ...(i)

Now, given ∠D = 90°

In quadrilateral PDQO,

∠OQD = ∠OPD = 90°    ...(angle between radius & tangent)

∴ ∠POQ = 90°, i.e., OPDQ is a regular polygon

Further DP = DQ, i.e., OPDQ is a square

Hence, radius = OP = DQ = 8cm   ...(ii)

Now, DC = DQ + QC

= 8 + 6

= 14cm   ...[from eqns. (i) and (ii)]