Advertisements
Advertisements
प्रश्न
The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds the angle of elevation becomes 300 If the aeroplane is flying at a constant height of 3000 3 m, find the speed of the aeroplane.
उत्तर
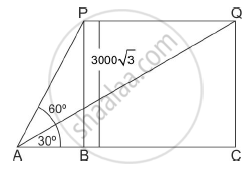
Let P and Q be the two positions of the plane and A be the point of observation. Let ABC be the horizontal line through A.
It is given that angles of elevation of the plane in two positions P and Q from a point A are 60° and 30° respectively.
∠PAB = 60°, ∠QAB = 30°. It is also given that PB = 3000√3 meters
In ΔABP, we have
`tan 60="BP"/"AB"`
`sqrt3/1=(3000sqrt3)/"AB"`
AB=3000m
In ΔACQ, we have
`tan 30="QC"/"AC"`
`1/sqrt3=(3000sqrt3)/"AC"`
AC = 9000 m
∴ Distance = BC = AC – AB = 9000m – 3000m = 6000m
Thus, the plane travels 6km in 30 seconds
Hence speed of plane = 6000/30 = 200 m/sec = 720km/h
APPEARS IN
संबंधित प्रश्न
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 90 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30°. The distance of the car from the tower (in metres) is
`(A) 50sqrt3`
`(B) 150sqrt 3`
`(C) 150sqrt2`
`(D) 75`
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car as an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 600. What is the height of the tower?
The shadow of a tower at a time is three times as long as its shadow when the angle of elevation of the sun is 60°. Find the angle of elevation of the sun at the time of the longer shadow ?
If the altitude of the sum is at 60°, then the height of the vertical tower that will cast a shadow of length 30 m is
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then find the width of the river.