Advertisements
Advertisements
प्रश्न
The angle of elevation of a cloud from a point h metre above a lake is θ. The angle of depression of its reflection in the lake is 45°. The height of the cloud is
पर्याय
h tan (45° + θ)
h cot (45° − θ)
h tan (45° − θ)
h cot (45° + θ)
उत्तर
Let AB be the surface of the lake and p be the point of observation. So AP=h . The given situation can be represented as,
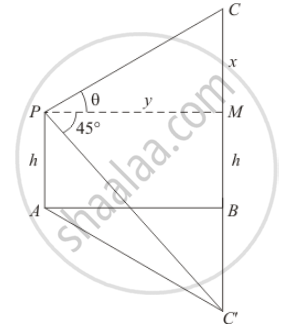
Here,C is the position of the cloud and C' is the reflection in the lake. Then .`CB=C'B`
Let PM be the perpendicular from P on CB. Then `∠CPM=θ` and .`∠C'PM=45°`
Let`CM=x` , `PM=y` , then`CB=x+h` and `C'B=x+h`
Here, we have to find the height of cloud.
So we use trigonometric ratios.
In , `ΔCMP`
`⇒ tan θ=(CM)/(PM)`
`⇒ tanθ=x/y`
`⇒ y= x/tanθ ` (1)
Again in ΔPMC',
`⇒ tan 45°=CM/PM`
`⇒1=(C'B+BM)/(PM)`
`⇒1=(x+h+h)/y`
`⇒y=x+2h`
`⇒ x/tanθ=x+2h` [using (1)]
`⇒ (x-x tanθ)/tan θ=2h`
`⇒ x=(2h tan θ)/((1-tan θ))`
Now,
`⇒ CB=h+x`
`⇒ CB=h+(2h tan θ)/(1-tan θ)`
`⇒ CB=(h(1-tanθ)+2h tanθ)/(1-tan θ)`
`⇒ CB= (h(1+tan θ))/(1-tan θ)=h tan(45°+ θ )` `[tan (A+B)=(tan A+tan B)/(1-tan A tan B)] `
APPEARS IN
संबंधित प्रश्न
A truck covers a distance of 150 km at a certain average speed and then covers another 200 km at an average speed which is 20 km per hour more than the first speed. If the truck covers the total distance in 5 hours, find the first speed of the truck.
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30°. Find the distance travelled by the balloon during the interval.

The ratio of the height of a tower and the length of its shadow on the ground is `sqrt3 : 1`. What is the angle of elevation of the sun?
On a straight line passing through the foot of a tower, two points C and D are at distances of 4 m and 16 m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower.
A TV tower stands vertically on a bank of a river/canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From a point 20 m away this point on the same bank, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the river/canal.
Two persons are a metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is
Two towers A and B are standing some distance apart. From the top of tower A, the angle of depression of the foot of tower B is found to be 30°. From the top of tower B, the angle of depression of the foot of tower A is found to be 60°. If the height of tower B is ‘h’ m then the height of tower A in terms of ‘h’ is ____________ m.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun ____________.
At a point on level ground, the angle of elevation of a vertical tower is, found to be α such that tan α = `1/3`. After walking 100 m towards the tower, the angle of elevation β becomes such that tan β = `3/4`. Find the height of the tower.
The angle of elevation of the top P of a vertical tower PQ of height 10 from a point A on the horizontal ground is 45°. Let R be a point on AQ and from a point B, vertically above R, the angle of elevation of P is 60°. If ∠BAQ = 30°, AB = d and the area of the trapezium PQRB is α, then the ordered pair (d, α) is ______.
