Advertisements
Advertisements
प्रश्न
A tower subtends an angle of 30° at a point on the same level as its foot. At a second point h metres above the first, the depression of the foot of the tower is 60°. The height of the tower is
पर्याय
\[\frac{h}{2} m\]
\[\sqrt{3h} m\]
\[\frac{h}{3} m\]
\[\frac{h}{\sqrt{3}}m\]
उत्तर
Let AB be the tower and C is a point on the same level as its foot such that ∠ACB = 30°
The given situation can be represented as,
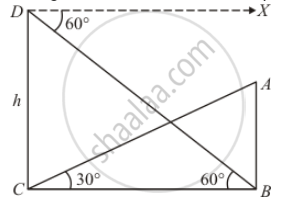
Here D is a point h m above the point C.
In ΔBCD,
`⇒ tan B=(CD)/(CB)`
`⇒ tan 60°=h/(CB)`
`⇒ sqrt3=h/(CB)`
`⇒ CB=h/sqrt3`
Again in triangle ABC,
`tan C=(AB)/(CB)`
`⇒ tan30= (AB)/((h/sqrt3))` [Using (1)]
`⇒1/sqrt3=AB/((h/sqrt3))`
`⇒ AB=h/3`
APPEARS IN
संबंधित प्रश्न
Two building are in front of each other on either side of a road of width 10 metres. From the top of the first building which is 40 metres high, the angle of elevation to the top of the second is 45°. What is the height of the second building?
A tower stands vertically on the ground. From a point on the ground which is 20 m away from the foot of the tower, the angle of elevation of its top is found to be 60°. Find the height of the tower. [Take `sqrt(3)` =1.732 ]
Two buildings are in front of each other on a road of width 15 meters. From the top of the first building, having a height of 12 meter, the angle of elevation of the top of the second building is 30°.What is the height of the second building?
The length of the shadow of a tower standing on level ground is found to be 2x metres longer when the sun's elevation is 30°than when it was 45°. The height of the tower in metres is
If a 1.5 m tall girl stands at a distance of 3 m from a lamp-post and casts a shadow of length 4.5 m on the ground, then the height of the lamp-post is
A ladder makes an angle of 60º with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is
If the ratio of the height of a tower and the length of its shadow is `sqrt(3): 1`, then the angle of elevation of the sun has measure
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 2m and is inclined at an angle of 30° to the ground. What should be the length of the slide?
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
|
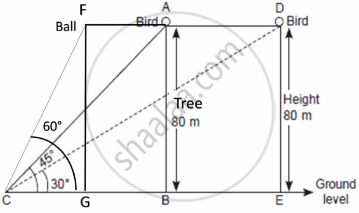
One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
|
- At what distance from the foot of the tree was he observing the bird sitting on the tree?
- How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball? - What is the speed of the bird in m/min if it had flown `20(sqrt3 + 1) m`?