Advertisements
Advertisements
प्रश्न
The length of the shadow of a tower standing on level ground is found to be 2x metres longer when the sun's elevation is 30°than when it was 45°. The height of the tower in metres is
पर्याय
\[\left( \sqrt{3} + 1 \right) x\]
\[\left( \sqrt{3} - 1 \right) x\]
\[2\sqrt{3}x\]
\[3\sqrt{2}x\]
उत्तर
Let h be the height of tower AB
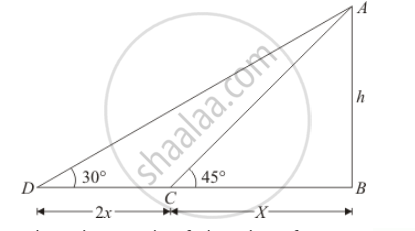
Given that: angle of elevation of sun are`∠D=30°` and.`∠C=45°`
Then Distance`CD=2x` and we assume `BC=x`Here, we have to find the height of tower.
So we use trigonometric ratios.
In a triangle,`ABC`
`⇒ tan C=(AB)/(BC)`
`⇒ tan 45°=(AB)/(BC)`
`⇒ 1=h/x`
`⇒ x=h`
Again in a triangle ABD,
`⇒ tan D= (AB)/(BC+CD)`
`⇒ tan 30°=h/( x+2x)`
`⇒1/sqrt3=h/(h+2x)` `[x=h]`
`⇒ sqrt3h=h+2x`
`h(sqrt3-1)=2x`
`⇒ h=2x/(sqrt3-1)`
⇒` h=(2x)/(sqrt3-1)xx(sqrt3+1)/(sqrt3+1)`
`⇒ h=x(sqrt3+1)`
APPEARS IN
संबंधित प्रश्न
The angle of elevation of a cliff from a fixed point is θ. After going up a distance of k metres towards the top of cliff at an angle of φ, it is found that the angle of elevation is α. Show that the height of the cliff is metres
The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance between the two buildings.
A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a so that it slides a distance b down the wall making an angle β with the horizontal. Show that `a/b = (cos alpha - cos beta)/(sin beta - sin alpha)`
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be a and 3. If the height of the lighthouse be h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance
`(h(tan alpha + tan beta))/(tan alpha tan beta)` meters
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
In the following figure, what are the angles of depression from the observing position O1 and O2of the object at A?
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
The angle of elevation of the top of a tower standing on a horizontal plane from a point A is α. After walking a distance d towards the foot of the tower the angle of elevation is found to be β. The height of the tower is
The angle of elevation of a cloud from a point h metre above a lake is θ. The angle of depression of its reflection in the lake is 45°. The height of the cloud is
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is 30°.
