Advertisements
Advertisements
प्रश्न
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
उत्तर
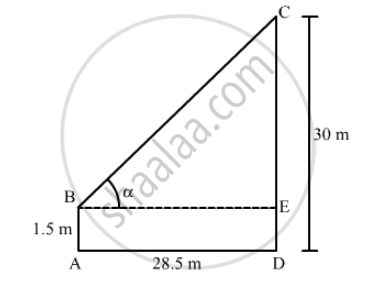
`"Let AB = 1.5 m be the observer and CD = 30 m be the tower."`
`"Let the angle of elevation of the top of the tower be α"`
`CD= CE+ED`
`⇒ CD=CE+AB`
`⇒30=CE+1.5`
`⇒CE=30-1.5=28.5 m`
In ΔCEB,
`tan ∝ = (CE)/(BE)=28.5/28.5`
`⇒ tan ∝ =1`
`⇒ tan ∝= tan 45° `
`⇒∝=45°`
APPEARS IN
संबंधित प्रश्न
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30°. The distance of the car from the tower (in metres) is
`(A) 50sqrt3`
`(B) 150sqrt 3`
`(C) 150sqrt2`
`(D) 75`
The angles of elevation of the top of a rock from the top and foot of a 100 m high tower are respectively 30° and 45°. Find the height of the rock.
The angle of depression form the top of a tower of a point A on the ground is 30° . On moving a distance of 20 meters from the point A towards the foot of the tower to a point B, the angle of elevation of the top of the tower to from the point B is 60° . Find the height of the tower and its distance from the point A.
If the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
Two persons are a metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 84 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between A and B. (tan 20° = 0.3640, `sqrt3` = 1.732)

Two persons are standing ‘x’ metres apart from each other and the height of the first person is double that of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the shorter person (in metres) is
The angles of elevation of the top of the rock from the top and foot of 100 m high tower are respectively 30° and 45°. The height of the rock is ____________.
Two pillars of equal lengths stand on either side of a road which is 100 m wide, exactly opposite to each other. At a point on the road between the pillars, the angles of elevation of the tops of the pillars are 60° and 30°. Find the length of each pillar and the distance of the point on the road from the pillars. (Use `sqrt3` = 1.732)
