Advertisements
Advertisements
प्रश्न
|
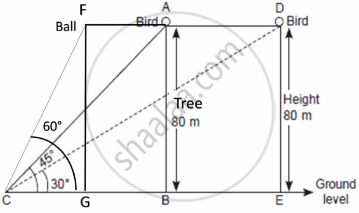
One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
|
- At what distance from the foot of the tree was he observing the bird sitting on the tree?
- How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball? - What is the speed of the bird in m/min if it had flown `20(sqrt3 + 1) m`?
उत्तर
i. tan 45° = `80/(CB)`
`\implies` CB = 80 m
ii. tan 30° = `80/(CE)`
`\implies 1/sqrt(3) = 80/(CE)`
`\implies` CE = `80sqrt(3)`
Distance the bird flew = AD = BE = CE – CB = `80sqrt(3) - 80 = 80(sqrt(3) - 1)m`
(or)
tan 60° = `80/(CG)`
`\implies sqrt(3) = 80/(CG)`
`\implies` CG = `80/sqrt(3)`
Distance the ball travelled after hitting the tree = FA = GB = CB – CG
GB = `80 - 80/sqrt(3)`
= `80(1 - 1/sqrt(3))m`
iii. Speed of the bird = `"Distance"/"Time taken"`
= `(20(sqrt(3) + 1))/2` m/sec
= `(20(sqrt(3) + 1))/2 xx 60` m/min
= `600(sqrt(3) + 1)` m/min
APPEARS IN
संबंधित प्रश्न
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
A tree standing on a horizontal plane is leaning towards the east. At two points situated at distances a and b exactly due west on it, the angles of elevation of the top are respectively α and β. Prove that the height of the top from the ground is `((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (take\[\sqrt{3}\]= 1.732)
The angle of elevation of a cloud from a point h metre above a lake is θ. The angle of depression of its reflection in the lake is 45°. The height of the cloud is
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiation control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms
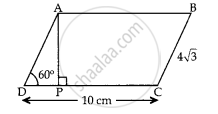
In given figure, ABCD is a || gm. The length of AP is ____________.
The tops of two poles of heights 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with the horizontal, then the length of the wire is ____________.
If two towers of heights h1 and h2 subtend angles of 60° and 30° respectively at the mid-point of the line joining their feet, then h1: h2 = ____________.
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top ____________.
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is ______.