Advertisements
Advertisements
प्रश्न
|
Tharunya was thrilled to know that the football tournament is fixed with a monthly timeframe from 20th July to 20th August 2023 and for the first time in the FIFA Women’s World Cup’s history, two nations host in 10 venues. Her father felt that the game can be better understood if the position of players is represented as points on a coordinate plane. |
- At an instance, the midfielders and forward formed a parallelogram. Find the position of the central midfielder (D) if the position of other players who formed the parallelogram are :- A(1, 2), B(4, 3) and C(6, 6)
- Check if the Goal keeper G(–3, 5), Sweeper H(3, 1) and Wing-back K(0, 3) fall on a same straight line.
[or]
Check if the Full-back J(5, –3) and centre-back I(–4, 6) are equidistant from forward C(0, 1) and if C is the mid-point of IJ. - If Defensive midfielder A(1, 4), Attacking midfielder B(2, –3) and Striker E(a, b) lie on the same straight line and B is equidistant from A and E, find the position of E.
उत्तर
i. Let D be (a, b), then
Mid point of AC = Midpoint of BD
`((1 + 6)/2, (2 + 6)/2) = ((4 + a)/2, (3 + b)/2)`
4 + a = 7
a = 3
3 + b = 8
b = 5
Central midfielder is at (3, 5)
ii. GH = `sqrt((-3 - 3)^2 + (5 - 1)^2`
= `sqrt(36 + 16)`
= `sqrt(52)`
= `2sqrt(13)`
GK = `sqrt((0 + 3)^2 + (3 - 5)^2`
= `sqrt(9 + 4)`
= `sqrt(13)`
HK = `sqrt((3 - 0)^2 + (1 - 3)^2`
= `sqrt(9 + 4)`
= `sqrt(13)`
GK + HK = GH `\implies` G,H and K lie on a same straight line
[or]
CJ = `sqrt((0 - 5)^2 + (1 + 3)^2`
= `sqrt(25 + 16)`
= `sqrt(41)`
CI = `sqrt((0 + 4)^2 + (1 - 6)^2`
= `sqrt(16 + 25)`
= `sqrt(41)`
Full-back J(5, –3) and centre-back I(–4, 6) are equidistant from forward C(0, 1)
Mid-point of IJ = `((5 - 4)/2, (-3 + 6)/2) = (1/2, 3/2)`
C is NOT the mid-point of IJ
iii. A, B and E lie on the same straight line and B is equidistant from A and E
⇒ B is the mid-point of AE
`((1 + a)/2, (4 + b)/2)` = (2, – 3)
1 + a = 4 ; a = 3.
4 + b = -6; b = –10 E is (3, –10)
APPEARS IN
संबंधित प्रश्न
If A(5, 2), B(2, −2) and C(−2, t) are the vertices of a right angled triangle with ∠B = 90°, then find the value of t.
Name the type of quadrilateral formed, if any, by the following point, and give reasons for your answer:
(4, 5), (7, 6), (4, 3), (1, 2)
If Q (0, 1) is equidistant from P (5, − 3) and R (x, 6), find the values of x. Also find the distance QR and PR.
If the distance between the points (4, k) and (1, 0) is 5, then what can be the possible values of k?
Determine whether the point is collinear.
R(0, 3), D(2, 1), S(3, –1)
Points A (-3, -2), B (-6, a), C (-3, -4) and D (0, -1) are the vertices of quadrilateral ABCD; find a if 'a' is negative and AB = CD.
Find the distance of the following points from origin.
(a cos θ, a sin θ).
Find distance between points O(0, 0) and B(– 5, 12)
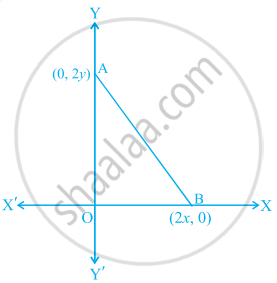
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is ______.
Case Study -2
A hockey field is the playing surface for the game of hockey. Historically, the game was played on natural turf (grass) but nowadays it is predominantly played on an artificial turf.
It is rectangular in shape - 100 yards by 60 yards. Goals consist of two upright posts placed equidistant from the centre of the backline, joined at the top by a horizontal crossbar. The inner edges of the posts must be 3.66 metres (4 yards) apart, and the lower edge of the crossbar must be 2.14 metres (7 feet) above the ground.
Each team plays with 11 players on the field during the game including the goalie. Positions you might play include -
- Forward: As shown by players A, B, C and D.
- Midfielders: As shown by players E, F and G.
- Fullbacks: As shown by players H, I and J.
- Goalie: As shown by player K.
Using the picture of a hockey field below, answer the questions that follow:
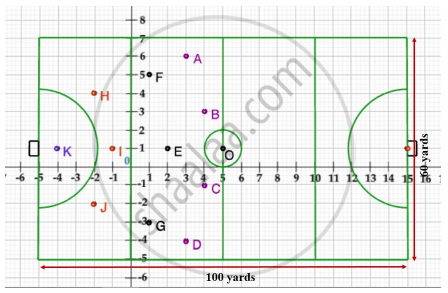
The point on x axis equidistant from I and E is ______.

