Advertisements
Advertisements
प्रश्न
As observed from the top of a light house 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° to 45°. Determine the distance travelled by the ship during this time. [Use `sqrt(3)` = 1.732]

उत्तर
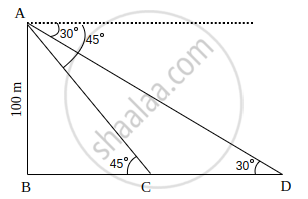
In ΔBD, ∠B = 90°
tan 30° = `("AB")/("BD")`
⇒ `1/sqrt(3) = 100/("BD")`
⇒ BD = `100sqrt(3)` m
In ΔBC, ∠B = 90°
tan 45° = `("AB")/("BC")`
⇒ 1 = `100/("BC")`
⇒ BC = 100 m
∴ Distance travelled by the ship = CD
= BD – BC
= `100sqrt(3) - 100`
= `100(sqrt(3) - 1)`
= 100 (1.732 - 1)
= 100 × 0.732
= 73.2 m ...(Approx)
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height of the flagstaff. [use √3=1.73]
An aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60º and 45º respectively. Find the vertical distance between the aeroplanes at that instant
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
The angle of elevation of the top of a tower at a point on the ground is 30º. What will be the angle of elevation, if the height of the tower is tripled?
AB is a pole of height 6 m standing at a point B and CD is a ladder inclined at angle of 600 to the horizontal and reaches upto a point D of pole . If AD = 2.54 m , find the length of the ladder.
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
Two persons are a metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is
If the angle of elevation of a cloud from a point ‘h’ metres above a lake is θ1 and the angle of depression of its reflection in the lake is θ2. Prove that the height that the cloud is located from the ground is `("h"(tan theta_1 + tan theta_2))/(tan theta_2 - tan theta_1)`
A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high tower observes two cars at angles of depression of 30° and 60°, which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars. (use `sqrt(3)` = 1.73)
