Advertisements
Advertisements
प्रश्न
The height of a tower is 100 m. When the angle of elevation of the sun changes from 30° to 45°, the shadow of the tower becomes x metres less. The value of x is
विकल्प
100 m
\[100\sqrt{3} m\]
\[100\left( \sqrt{3} - 1 \right) m\]
\[\frac{100}{3}m\]
उत्तर
The given situation can be represented as,
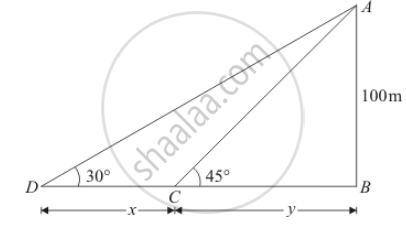
Here, AB is the tower of height 100 meters.
When angle of elevation of sun changes from`∠D=30°` to `∠C=45°`, .`CD=x`
We assumed that `BC=y`
Here we have to find the value of x
So we use trigonometric ratios.
In a triangle,`ABC`
`⇒ tan C=(AB)/(BC)`
`⇒ tan 45°=(AB)/(BC)`
`⇒1=100/y`
`⇒y=100`
Again in a triangle ABD,
`⇒ tan D=( AB)/(BC+CD)`
`⇒ tan 30°=100/(x+y)`
`⇒ 1/sqrt3=100/(x+y)`
`⇒ 100sqrt3=x+y`
`⇒100sqrt3=x+100` `Put x=100`
`⇒x=100(sqrt3-1)`
APPEARS IN
संबंधित प्रश्न
A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/h.
A man sitting at a height of 20 m on a tall tree on a small island in the middle of a river observes two poles directly opposite to each other on the two banks of the river and in line with the foot of the tree. If the angles of depression of the feet of the poles from a point at which the man is sitting on the tree on either side of the river are 60° and 30°respectively. Find the width of the river.
Two men are on opposite side of tower. They measure the angles of elevation of the top of the tower as 30 and 45 respectively. If the height of the tower is 50 meters, find the distance between the two men.
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
If the ratio of the height of a tower and the length of its shadow is `sqrt(3): 1`, then the angle of elevation of the sun has measure
A Technician has to repair light on a pole of height 10 m. She needs to reach a point 1 m below the top of the pole to undertake the repair work. What should be the length of the ladder that she should use which, when inclined at an angle of 60∘ to the ground, would enable her to reach the required position? Also, how far from the foot of the pole should she place the foot of the ladder?
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top ____________.
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
From the top of an 8 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Take `sqrt(3)` = 1.732).
Two circles of radii 5 cm and 3 cm touch each other externally. Find the distance between their centres.
