Advertisements
Advertisements
प्रश्न
From the top of an 8 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Take `sqrt(3)` = 1.732).
उत्तर
According to given information, we have the following figure
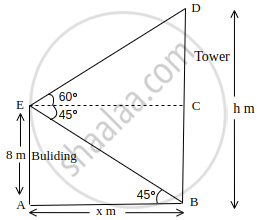
Let BD = h m and AB = x m
Then, CD = h – 8 ...(∵ BC = 8 m)
Also, In ΔEAB, we have
tan45° = `8/x`
⇒ 1 = `8/x`
⇒ x = 8 m
Similarly, In ΔDCE, we have
tan60° = `(CD)/(EC)`
⇒ `sqrt(3) = (h - 8)/x` ...(∵ EC = AB = x m)
⇒ `sqrt(3)x` = h – 8
⇒ `8sqrt(3)` = h – 8 ...(∵ x = 8 m)
⇒ h = `8(sqrt(3) + 1)`
= 8 × 2.732
= 21.856 m
APPEARS IN
संबंधित प्रश्न
An aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60º and 45º respectively. Find the vertical distance between the aeroplanes at that instant
The angle of elevation of an aeroplane from a point on the ground is 45° after flying for 15seconds, the elevation changes to 30° . If the aeroplane is flying at a height of 2500 meters, find the speed of the areoplane.
The angle of elevation of the top of a tower from ta point on the same level as the foot of the tower is 30° . On advancing 150 m towards foot of the tower, the angle of elevation becomes 60° Show that the height of the tower is 129.9 metres.
From the top of a vertical tower, the angles depression of two cars in the same straight line with the base of the tower, at an instant are found to be 45° and 60° . If the cars are 100 m apart and are on the same side of the tower, find the height of the tower.
From the top of the light house, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the light-house is 100 meters, then find how far the ship is from the light-house.
A tower subtends an angle of 30° at a point on the same level as its foot. At a second point h metres above the first, the depression of the foot of the tower is 60°. The height of the tower is
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the height of the lamp post
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is 30°.
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60°, then the distance between the two towers is ____________.
Find the length of the shadow on the ground of a pole of height 18m when angle of elevation θ of the sun is such that tan θ = `6/7`.
