Advertisements
Advertisements
प्रश्न
Two persons are a metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is
विकल्प
\[\frac{a}{4}\]
\[\frac{a}{\sqrt{2}}\]
\[a\sqrt{2}\]
\[\frac{a}{2\sqrt{2}}\]
उत्तर
Let AB and CD be the two persons such that AB < CD.
Then, let AB = h so that CD = 2h
Now, the given information can be represented as,
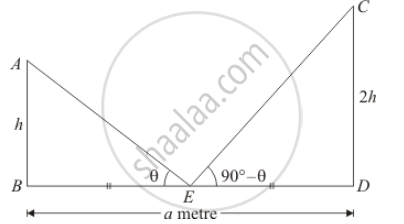
Here, E is the midpoint of BD.
We have to find height of the shorter person.
So we use trigonometric ratios.
In triangle ECD,
`tan ∠ CED=(CD)/(ED)`
`⇒ tan (90°-θ)=(2h)/((a/2))`
`⇒ cot θ=(4h)/a`
Again in triangle ABE,
`⇒tan ∠AEB=(AB)/(BE)`
`⇒tanθ=h/((a/2))`
`⇒ 1/cot θ=(2h)/a`
`⇒a/(4h)=(2h)/a`
`⇒a^2=8h^2`
`⇒ h=a/(2sqrt2)`
APPEARS IN
संबंधित प्रश्न
A ladder makes an angle of 60° with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is:
(A) `4/sqrt3`
(B) `4sqrt3`
(C) `2sqrt2`
(D)4
A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.

The angle of elevation of the top of a chimney form the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30° . If the height of the tower is 40 meters. Find the height of the chimney.
A solid right-circular cone of height 60 cm and radius 30 cm is dropped in a right-circular cylinder full of water of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres ?
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
The electric pole subtends an angle of 30° at a point on the same level as its foot. At a second point ‘b’ metres above the first, the depression of the foot of the pole is 60°. The height of the pole (in metres) is equal to
The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
If one looks from a tower 10 m high at the top of a flag staff, the depression angle of 30° is made. Also, looking at the bottom of the staff from the tower, the angle of the depression made is of 60°. Find the height of the flag staff.
