Advertisements
Advertisements
प्रश्न
A ladder makes an angle of 60° with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is:
(A) `4/sqrt3`
(B) `4sqrt3`
(C) `2sqrt2`
(D)4
उत्तर
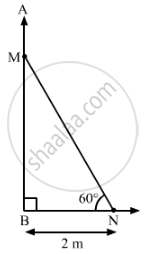
In the figure, MN is the length of the ladder, which is placed against the wall AB and makes an angle of 60° with the ground.
The foot of the ladder is at N, which is 2 m away from the wall.
∴ BN = 2 m
In right-angled triangle MNB:
`"Number of favourable outcomes"/"Total number of outcomes"=3/4`
Therefore, the length of the ladder is 4 m.
Hence, the correct option is D.
APPEARS IN
संबंधित प्रश्न
A person standing on the bank of river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find the height of the tree and width of the river. `(sqrt 3=1.73)`
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45. Find the height of the tower PQ and the distance PX. (Use `sqrt3=1.73)`
The altitude of the sun at any instant is 60º. Find the height of the vertical pole that will cast a shadow of 30 m.
The angle of elevation of an aeroplane from a point on the ground is 45° after flying for 15seconds, the elevation changes to 30° . If the aeroplane is flying at a height of 2500 meters, find the speed of the areoplane.
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket. [Use`pi22/7` ]
The angle of elevation of the top of a tower at a point on the ground is 30º. What will be the angle of elevation, if the height of the tower is tripled?
Two buildings are in front of each other on either side of a road of width 10 metres. From the top of the first building which is 20 metres high, the angle of elevation to the top of the second is 45°. What is the height of the second building?
As observed from the top of a 150 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
From the top of building AB, a point C is observed on the ground whose angle of depression is 60° and which is at a distance of 40 m from the base of the building. Complete the following activity to find the height of building AB.

From figure, BC = `square`, ∠ACB = `square`
In ΔACB,
tan `square = square/(BC)`
⇒ `square = square/square`
⇒ `square = square`
Hence, the height of the building AB is `square`.
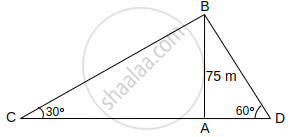
Two men on either side of a cliff 75 m high observe the angles of elevation of the top of the cliff to be 30° and 60°. Find the distance between the two men.