Advertisements
Advertisements
प्रश्न
Two men are on opposite side of tower. They measure the angles of elevation of the top of the tower as 30 and 45 respectively. If the height of the tower is 50 meters, find the distance between the two men.
उत्तर
Let CD be the tower and A and B be the positions of the two men standing on the opposite sides.
Thus, we have:
∠DAC = 30°, ∠DBC = 45° and CD = 50 m
Let AB = xmand BC = ymsuch that AC = (x - y)m.
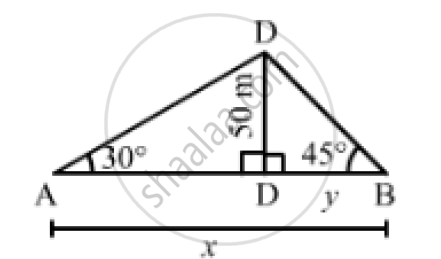
In the right ΔDBC,we have:
`(CD)/(BC) = tan 45° = 1`
`⇒ 50/y = 1`
⇒ y = 50 m
In the right ΔACD,we have:
`(CD)/(AC) = tan 30° = 1/ sqrt(3) `
`⇒ 50/ ((x-y)) = 1/ sqrt(3)`
`x -y = 50 sqrt(3)`
On putting y = 50in the above equation, we get:
`x -50= 50sqrt(3)`
`⇒ x = 50 + 50 sqrt(3) = 50 ( sqrt(3) +1) = 136.6m `
∴Distance between the two men = AB = x = 136.6m
APPEARS IN
संबंधित प्रश्न
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 90 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
From the top of a building 30 m high, the top and bottom of a tower are observed to have angles of depression 30º and 45º respectively. Find the height of the tower
The heights of two poles are 80 m and 62.5 m. If the line joining their tops makes an angle of 45º with the horizontal, then find the distance between the pole
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
The angle of elevation of the top of a tower as observed form a point in a horizontal plane through the foot of the tower is 32°. When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to be 63°. Find the height of the tower and the distance of the first position from the tower. [Take tan 32° = 0.6248 and tan 63° = 1.9626]
The horizontal distance between two buildings is 70 m. The angle of depression of the top of the first building when seen from the top of the second building is 45°. If the height of the second building is 120 m, find the height of the first building
The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is
The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 20 meters towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower ____________.
A pole of height 30 m is observed from a point. The angle of depression of the point is 30°. Find the distance of the point from the base of the pole.
Two circles of radii 5 cm and 3 cm touch each other externally. Find the distance between their centres.
