Advertisements
Advertisements
प्रश्न
From the point of a tower 100m high, a man observe two cars on the opposite sides to the tower with angles of depression 30° and 45 respectively. Find the distance between the cars
उत्तर
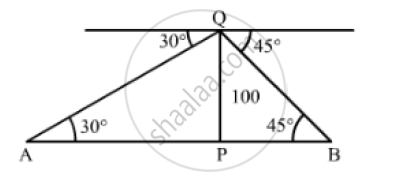
Let PQ be the tower
We have,
PQ = 100m, ∠PQR = 30° and ∠PBQ = 45°
In ΔAPQ,
`tan 30° = (PQ)/(AP)`
`⇒ 1/ sqrt(3) = 100/(AP)`
`⇒AP = 100 sqrt(3) m`
Also, in ΔBPQ,
` tan 45° = (PQ)/(BP)`
`⇒ 1 = 100/(BP)`
⇒ BP = 100M
Now , AB = AP+ BP
`= 100 sqrt(3) + 100`
`= 100( sqrt(3) +1)`
`= 100 xx (1.73 +1 )`
` = 100 xx 2.73`
= 273 m
So, the distance between the cars is 273m.
APPEARS IN
संबंधित प्रश्न
If the angle of elevation of cloud from a point 200 m above a lake is 30º and the angle of depression of its reflection in the lake is 60º, then find the height of the cloud above the lake
A man on a cliff observes a fishing trawler at an angle of depression of 30º which is approaching the shore to the point immediately beneath the observer with a uniform speed. 6 minutes later, the angle of depression of the trawler is found to be 60º. Caliculate the time taken by the trawler to reach the shore
An aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60º and 45º respectively. Find the vertical distance between the aeroplanes at that instant
A tree standing on a horizontal plane is leaning towards the east. At two points situated at distances a and b exactly due west on it, the angles of elevation of the top are respectively α and β. Prove that the height of the top from the ground is `((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a so that it slides a distance b down the wall making an angle β with the horizontal. Show that `a/b = (cos alpha - cos beta)/(sin beta - sin alpha)`
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be a and 3. If the height of the lighthouse be h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance
`(h(tan alpha + tan beta))/(tan alpha tan beta)` meters
In given figure, the length of AP is ____________.

As observed from the top of a 150 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Two towers A and B are standing some distance apart. From the top of tower A, the angle of depression of the foot of tower B is found to be 30°. From the top of tower B, the angle of depression of the foot of tower A is found to be 60°. If the height of tower B is ‘h’ m then the height of tower A in terms of ‘h’ is ____________ m.
Two vertical poles of different heights are standing 20m away from each other on the level ground. The angle of elevation of the top of the first pole from the foot of the second pole is 60° and angle of elevation of the top of the second pole from the foot of the first pole is 30°. Find the difference between the heights of two poles. (Take `sqrt(3)` = 1.73)
