Advertisements
Advertisements
प्रश्न
From the point of a tower 100m high, a man observe two cars on the opposite sides to the tower with angles of depression 30° and 45 respectively. Find the distance between the cars
उत्तर
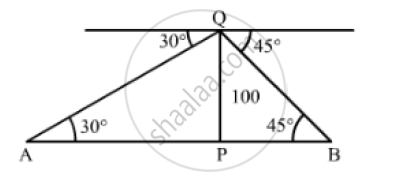
Let PQ be the tower
We have,
PQ = 100m, ∠PQR = 30° and ∠PBQ = 45°
In ΔAPQ,
`tan 30° = (PQ)/(AP)`
`⇒ 1/ sqrt(3) = 100/(AP)`
`⇒AP = 100 sqrt(3) m`
Also, in ΔBPQ,
` tan 45° = (PQ)/(BP)`
`⇒ 1 = 100/(BP)`
⇒ BP = 100M
Now , AB = AP+ BP
`= 100 sqrt(3) + 100`
`= 100( sqrt(3) +1)`
`= 100 xx (1.73 +1 )`
` = 100 xx 2.73`
= 273 m
So, the distance between the cars is 273m.
APPEARS IN
संबंधित प्रश्न
The angle of elevation of a cliff from a fixed point is θ. After going up a distance of k metres towards the top of cliff at an angle of φ, it is found that the angle of elevation is α. Show that the height of the cliff is metres
If the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
When an observer at a distance of 12 m from a tree looks at the top of the tree, the angle of elevation is 60°. What is the height of the tree? `(sqrt 3 = 1.73)`
To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? `(sqrt(3) = 1.732)`
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 2m and is inclined at an angle of 30° to the ground. What should be the length of the slide?
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Then the height of the tower is ____________.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point, 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
Let AB and PQ be two vertical poles, 160 m apart from each other. Let C be the middle point of B and Q, which are feet of these two poles. Let `π/8` and θ be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then, tan2 θ is equal to ______.
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is ______.
