Advertisements
Advertisements
प्रश्न
When an observer at a distance of 12 m from a tree looks at the top of the tree, the angle of elevation is 60°. What is the height of the tree? `(sqrt 3 = 1.73)`
उत्तर
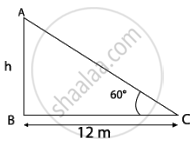
tan 60° = `"AB"/"BC"`
`sqrt 3 = "h"/12`
`therefore "h" = 12 sqrt 3` m
= 12 × 1.73 m
h = 20.76 m
APPEARS IN
संबंधित प्रश्न
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30°. The distance of the car from the tower (in metres) is
`(A) 50sqrt3`
`(B) 150sqrt 3`
`(C) 150sqrt2`
`(D) 75`
Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships as observed from the top of the light house are 60° and 45°. If the height of the light house is 200 m, find the distance between the two ships. [use √3=1.73]
The angles of elevation and depression of the top and the bottom of a tower from the top of a building, 60 m high, are 30° and 60° respectively. Find the difference between the heights of the building and the tower and the distance between them.
A ladder against a vertical wall makes an angle of 45º with the ground. The foot of the ladder is 3m from the wall. Find the length of the ladder
The heights of two poles are 80 m and 62.5 m. If the line joining their tops makes an angle of 45º with the horizontal, then find the distance between the pole
A tower is 100√3 metres high. Find the angle of elevation of its top from a point 100 metres away from its foot.
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30°. Find the distance travelled by the balloon during the interval.

On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance between the two buildings.
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
A ladder of length 6meters makes an angle of 45° with the floor while leaning against one wall of a room. If the fort of the ladder is kept fixed on the floor and it is made to lean against the opposite wall of the room, it makes an angle of 60° with the floor. Find the
distance between two walls of the room.
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angels of elevation of the top of the poles are 60° and 30° respectively.
Find the height of the poles and the distances of the point from the poles.
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find radius of the dome `(sqrt(3) = 1.732)`
A man is standing on the deck of a ship, which is 40 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill `(sqrt(3) = 1.732)`
The angles of elevation of the top of the rock from the top and foot of 100 m high tower are respectively 30° and 45°. The height of the rock is ____________.
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Then the height of the tower is ____________.
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is ______.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30°. Determine the height of the tower.
