Advertisements
Advertisements
प्रश्न
Two men are on opposite side of tower. They measure the angles of elevation of the top of the tower as 30 and 45 respectively. If the height of the tower is 50 meters, find the distance between the two men.
उत्तर
Let CD be the tower and A and B be the positions of the two men standing on the opposite sides.
Thus, we have:
∠DAC = 30°, ∠DBC = 45° and CD = 50 m
Let AB = xmand BC = ymsuch that AC = (x - y)m.
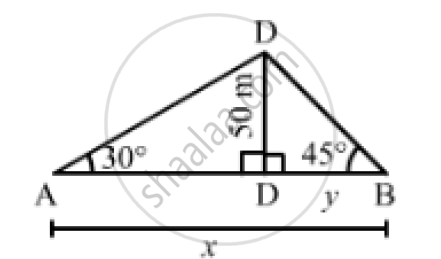
In the right ΔDBC,we have:
`(CD)/(BC) = tan 45° = 1`
`⇒ 50/y = 1`
⇒ y = 50 m
In the right ΔACD,we have:
`(CD)/(AC) = tan 30° = 1/ sqrt(3) `
`⇒ 50/ ((x-y)) = 1/ sqrt(3)`
`x -y = 50 sqrt(3)`
On putting y = 50in the above equation, we get:
`x -50= 50sqrt(3)`
`⇒ x = 50 + 50 sqrt(3) = 50 ( sqrt(3) +1) = 136.6m `
∴Distance between the two men = AB = x = 136.6m
APPEARS IN
संबंधित प्रश्न
A person standing on the bank of river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find the height of the tree and width of the river. `(sqrt 3=1.73)`
A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level
If a tower 30 m high, casts a shadow `10sqrt3` m long on the ground, then what is the angle of elevation of the sun?
From the top of a lighthouse, an observer looking at a ship makes angle of depression of 60°. If the height of the lighthouse is 90 metre, then find how far the ship is from the lighthouse.
From the top of the tower h metre high , the angles of depression of two objects , which are in the line with the foot of the tower are ∝ and ß (ß> ∝ ) cts .
What is the angle of elevation of the Sun when the length of the shadow of a vetical pole is equal to its height?
If the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find radius of the dome `(sqrt(3) = 1.732)`
A pole of height 30 m is observed from a point. The angle of depression of the point is 30°. Find the distance of the point from the base of the pole.
From the top of an 8 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Take `sqrt(3)` = 1.732).
