Advertisements
Advertisements
प्रश्न
A person standing on the bank of river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find the height of the tree and width of the river. `(sqrt 3=1.73)`
उत्तर १
Let AB = height of the tower = h metres
In the right angled ΔABC and right angled ΔABD,
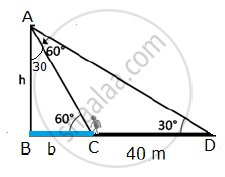
`tan60^@=h/(BC)=sqrt(3) rArr BC=h/sqrt(3)`
`tan30^@=h/(BD)=1/sqrt(3) rArr BD=hsqrt(3)`
`Now, BD – BC = 40`
`hsqrt(3)-h/sqrt(3)=40`
`(3h-h)/sqrt3=40`
`2h=40sqrt3`
`h=20sqrt3 m`
In right angled ΔABC,
`tan30°=1/sqrt3`
`(BC)/h=1/sqrt3`
`(BC)/(20sqrt3)=1/sqrt3`
`BC=b=20m`
Width of the river = BC = 20 m
Thus, the height of the tree is `20 sqrt3` metres and width of the river is 20 metres.
उत्तर २
Let BC be the height of the tree.
AB be the breadth of the river.
A be the initial position of the person
D be the final position of the person
∠CAB = 60° & ∠CDB = 30° & DA = 40m
Let AB = x & BC = h
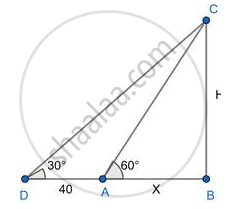
In Δ DBC
⇒ `tan 30 = "BC"/"DB" = "BC"/"DA+AB" ="h"/(40+"x")`
⇒ `1/sqrt3 = "h"/(40+"x")`
⇒ `"h" = 40+"x"/sqrt3` ................(1)
In Δ ABC
⇒ `tan60 = "BC"/"AB"="h"/"x"`
⇒ `sqrt3 = "h"/"x"`
⇒ `"h"=sqrt3 "x"` ..................(2)
Using (1) & (2)
`"h"=(40+"x")/sqrt3`
⇒ `sqrt(3"x")=(40+"x")/sqrt3`
⇒ 3x =40 + x
⇒ 2x = 40
⇒ x = 20
⇒ AB = 20m
⇒ BC = `20sqrt3` m =20 ×1.73 =34.6m
∴ Height of the tree is 34.6m and the width of the river is 20m.
उत्तर ३

Consider the above diagram where AB is the height of a tree with point A as the top of the tree
Point B base of the tree
Initially, the person is at point C, therefore, BC is the width of the river and the person observes the angle of elevation to be 60° i.e. ∠ACB = 60°
The person moves 40 m away from the bank of the rives thus the new position of the person is point D and CD = 40m
From D the person observes the angle of elevation to be 30° i.e. ∠ADB = 30°
Consider ∆ABC
tan60° = `"AB"/"BC"`
∴AB = `"BC"sqrt3` …(i)
Consider ∆ABD
tan30° = `"AB"/"BD"`
`1/sqrt(3) = "AB"/("BC + CD")`
Using CD = 40 m
(BC + 40) = `"AB"sqrt3`
∴ AB = `("BC" + 40)/sqrt3` …(ii)
From (i) and (ii)
`"BC"sqrt3` = `("BC" + 40)/sqrt3`
∴ `"BC"sqrt(3) xx sqrt(3) = "BC" + 40`
∴ 3BC = BC + 40
∴ 2BC = 40
∴ BC = 20 m
Therefore width of the river = BC = 20 m
Substituting BC in equation (i)
AB = `20sqrt3`
∴ AB = 20 × 1.73
∴ AB = 34.6 m
Therefore height of tree = AB = 34.6 m
Hence height of tree is 34.6 meters and width of river is 20 meters
संबंधित प्रश्न
The angles of elevation and depression of the top and the bottom of a tower from the top of a building, 60 m high, are 30° and 60° respectively. Find the difference between the heights of the building and the tower and the distance between them.
The angle of elevation of an aeroplane from a point on the ground is 45° after flying for 15seconds, the elevation changes to 30° . If the aeroplane is flying at a height of 2500 meters, find the speed of the areoplane.
As observed form the top of a lighthouse, 100m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° and 60° . Determine the distance travelled by the ship during the period of observation.
A ladder 15 m long makes an angle of 60° with the wall. Find the height of the point where the ladder touches the wall.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (take\[\sqrt{3}\]= 1.732)
The length of shadow of a tower on the plane ground is `sqrt3` times the height of the tower.
The angle of elevation of sun is:
Two buildings are in front of each other on a road of width 15 meters. From the top of the first building, having a height of 12 meter, the angle of elevation of the top of the second building is 30°.What is the height of the second building?
The angle of elevation of the top of a tower standing on a horizontal plane from a point A is α. After walking a distance d towards the foot of the tower the angle of elevation is found to be β. The height of the tower is
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart. the height of the light house is
When an observer at a distance of 12 m from a tree looks at the top of the tree, the angle of elevation is 60°. What is the height of the tree? `(sqrt 3 = 1.73)`
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is `200[(sqrt(3) + 1)/sqrt(3)]` metres, find the height of the lighthouse.
In given figure, ABCD is a || gm. The length of AP is ____________.
The upper part of a tree is broken by the wind and makes an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 5 m. The height of the tree is ____________.
A vertical pole of 30 m is fixed on a tower. From a point on the level ground, the angle of elevation of the top and bottom of the pole is 60° and 45°. Find the height of the tower.
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top ____________.
There are two windows in a house. A window of the house is at a height of 1.5 m above the ground and the other window is 3 m vertically above the lower window. Ram and Shyam are sitting inside the two windows. At an instant, the angle of elevation of a balloon from these windows is observed as 45° and 30° respectively. Find the height of the balloon from the ground.
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.
An aeroplane when flying at a height of 3125 m from the ground passes vertically below another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 30° and 60° respectively. Find the distance between the two planes at that instant.
A person is standing at a distance of 50 m from a temple looking at its top. The angle of elevation is 45°. Find the height of the temple.
Two pillars of equal lengths stand on either side of a road which is 100 m wide, exactly opposite to each other. At a point on the road between the pillars, the angles of elevation of the tops of the pillars are 60° and 30°. Find the length of each pillar and the distance of the point on the road from the pillars. (Use `sqrt3` = 1.732)
