Advertisements
Advertisements
प्रश्न
As observed form the top of a lighthouse, 100m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° and 60° . Determine the distance travelled by the ship during the period of observation.
उत्तर
Let OA be the lighthouse and B and C be the positions of the ship.
Thus, we have:
OA = 100m, ∠OBA = 30° and ∠OCA = 60°
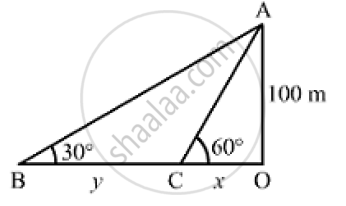
Let
OC = xmand BC = ym
In the right ΔOAC,we have
`(OA)/(OC) = tan 60° = sqrt(3) `
`⇒100/x = sqrt(3)`
`⇒ x = 100/sqrt(3) m`
Now, in the right ΔOBA,we have:
`(OA)/(OB) =tan 30° = 1/ sqrt(3)`
`⇒ 100/(x+y) = 1/ sqrt(3)`
`⇒ x+ y = 100 sqrt(3) `
On putting `x = 100/ sqrt(3)` in the above equation, we get:
`y = 100 sqrt(3) - 100/sqrt(3) = (300-100)/ sqrt(3) = 200/sqrt(3) = 115.47 m`
∴Distance travelled by the ship during the period of observation = B = y =115.47m
APPEARS IN
संबंधित प्रश्न
If the elevation of the sun changed from 30º to 60º, then find the difference between the lengths of shadows of a pole 15 m high, made at these two positions
The elevation of a tower at a station A due north of it is α and at a station B due west of A is β. Prove that the height of the tower is `\frac{AB\sin \alpha \sin \beta }{\sqrt{\sin^{2}\alpha -\sin ^{2}\beta `
A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60°. to the horizontal. Find the length of the string, assuming that there is no slack in it.
[Take `sqrt(3)` =1.732 ]
From the top of a tower of height 50 m, the angles of depression of the top and bottom of a pole are 30° and 45° respectively. Find
(i) how far the pole is from the bottom of a tower,
(ii) the height of the pole. (Use \[\sqrt{3} = 1 . 732\])
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
A kite is flying at a height of 30 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
A pole of height 30 m is observed from a point. The angle of depression of the point is 30°. Find the distance of the point from the base of the pole.
Find the length of the shadow on the ground of a pole of height 18m when angle of elevation θ of the sun is such that tan θ = `6/7`.
Two circles of radii 5 cm and 3 cm touch each other externally. Find the distance between their centres.
