Advertisements
Advertisements
प्रश्न
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 2.5m from the banks, find the width of the river.
उत्तर
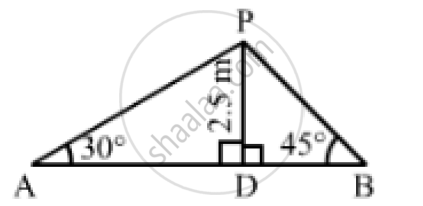
Let A and B be two points on the banks on the opposite side of the river and P be the point on the bridge at a height of 2.5 m.
Thus, we have:
DP = 2.5, ∠PAD = 30° and ∠PBD = 45°
In the right ΔAPD,we have:
`(DP)/(AD) = tan 30° = 1/sqrt(3)`
`⇒ 2.5 /(AD) = 1/ sqrt(3)`
`⇒ AD = 2.5 sqrt(3) m`
In the right ΔPDB,we have:
`(DP)/(BD) = tan 45° = 1`
`⇒ 2.5/(BD) = 1`
⇒ BD=2.5m
`∴"Width of the river" = AB = ( AD+ BD) =(2.5sqrt(3) + 2.5) = 6.83m`
APPEARS IN
संबंधित प्रश्न
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.

From the top of a tower, 100, high, a man observes two cars on the opposite sides of the tower and in same straight line with its base, with angles of depression 30° and 45°. Find the distance between the cars. [Take `sqrt3` = 1.732]
Two men are on opposite side of tower. They measure the angles of elevation of the top of the tower as 30 and 45 respectively. If the height of the tower is 50 meters, find the distance between the two men.
The angle of elevation on the top of a building from the foot of a tower is 30° . The angle of elevation of the top of the tower when seen from the top of the second water is 60° .If the tower is 60m high, find the height of the building.
A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45º. Then the height of the tower (in metres) is
A Technician has to repair light on a pole of height 10 m. She needs to reach a point 1 m below the top of the pole to undertake the repair work. What should be the length of the ladder that she should use which, when inclined at an angle of 60∘ to the ground, would enable her to reach the required position? Also, how far from the foot of the pole should she place the foot of the ladder?
A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are α and β, respectively. Then the height of the tower is ____________.
A pole of height 30 m is observed from a point. The angle of depression of the point is 30°. Find the distance of the point from the base of the pole.
