Advertisements
Advertisements
प्रश्न
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
उत्तर
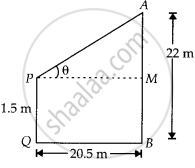
Let the angle of elevation of the top of the tower from the eye of the observer is θ
Given that,
AB = 22 m,
PQ = 1.5 m = MB
And QB = PM = 20.5 m
⇒ AM = AB – MB
= 22 – 1.5
= 20.5 m
Now, In ∆APM,
tan θ = `"AM"/"PM" = 20.5/20.5` = 1
⇒ tan θ = tan 45°
∴ θ = 45°
Hence, the required angle of elevation of the top of the tower from the eye of the observer is 45°.
APPEARS IN
संबंधित प्रश्न
From the top of a tower of height 50 m, the angles of depression of the top and bottom of a pole are 30° and 45° respectively. Find
(i) how far the pole is from the bottom of a tower,
(ii) the height of the pole. (Use \[\sqrt{3} = 1 . 732\])
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket. [Use`pi22/7` ]
While landing at an airport, a pilot made an angle of depression of 20°. Average speed of the plane was 200 km/hr. The plane reached the ground after 54 seconds. Find the height at which the plane was when it started landing. (sin 20° = 0.342)
A storm broke a tree and the tree top rested on ground 20 m away from the
base of the tree, making an angle of 60o with the ground. Find the height
of the tree.
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
On a morning walk, three persons step out together and their steps measure 30 cm, 36 cm, and 40 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
In given figure, ABCD is a || gm. The length of AP is ____________.
From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α). Find the distance between the two objects.
A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h(1+ tan α tan β) metres.
The angle of elevation of the top P of a vertical tower PQ of height 10 from a point A on the horizontal ground is 45°. Let R be a point on AQ and from a point B, vertically above R, the angle of elevation of P is 60°. If ∠BAQ = 30°, AB = d and the area of the trapezium PQRB is α, then the ordered pair (d, α) is ______.
