Advertisements
Advertisements
Question
A person standing on the bank of river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find the height of the tree and width of the river. `(sqrt 3=1.73)`
Solution 1
Let AB = height of the tower = h metres
In the right angled ΔABC and right angled ΔABD,
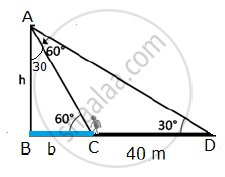
`tan60^@=h/(BC)=sqrt(3) rArr BC=h/sqrt(3)`
`tan30^@=h/(BD)=1/sqrt(3) rArr BD=hsqrt(3)`
`Now, BD – BC = 40`
`hsqrt(3)-h/sqrt(3)=40`
`(3h-h)/sqrt3=40`
`2h=40sqrt3`
`h=20sqrt3 m`
In right angled ΔABC,
`tan30°=1/sqrt3`
`(BC)/h=1/sqrt3`
`(BC)/(20sqrt3)=1/sqrt3`
`BC=b=20m`
Width of the river = BC = 20 m
Thus, the height of the tree is `20 sqrt3` metres and width of the river is 20 metres.
Solution 2
Let BC be the height of the tree.
AB be the breadth of the river.
A be the initial position of the person
D be the final position of the person
∠CAB = 60° & ∠CDB = 30° & DA = 40m
Let AB = x & BC = h
In Δ DBC
⇒ `tan 30 = "BC"/"DB" = "BC"/"DA+AB" ="h"/(40+"x")`
⇒ `1/sqrt3 = "h"/(40+"x")`
⇒ `"h" = 40+"x"/sqrt3` ................(1)
In Δ ABC
⇒ `tan60 = "BC"/"AB"="h"/"x"`
⇒ `sqrt3 = "h"/"x"`
⇒ `"h"=sqrt3 "x"` ..................(2)
Using (1) & (2)
`"h"=(40+"x")/sqrt3`
⇒ `sqrt(3"x")=(40+"x")/sqrt3`
⇒ 3x =40 + x
⇒ 2x = 40
⇒ x = 20
⇒ AB = 20m
⇒ BC = `20sqrt3` m =20 ×1.73 =34.6m
∴ Height of the tree is 34.6m and the width of the river is 20m.
Solution 3

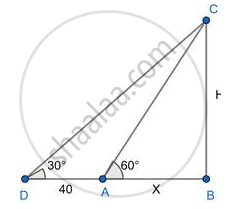
Consider the above diagram where AB is the height of a tree with point A as the top of the tree
Point B base of the tree
Initially, the person is at point C, therefore, BC is the width of the river and the person observes the angle of elevation to be 60° i.e. ∠ACB = 60°
The person moves 40 m away from the bank of the rives thus the new position of the person is point D and CD = 40m
From D the person observes the angle of elevation to be 30° i.e. ∠ADB = 30°
Consider ∆ABC
tan60° = `"AB"/"BC"`
∴AB = `"BC"sqrt3` …(i)
Consider ∆ABD
tan30° = `"AB"/"BD"`
`1/sqrt(3) = "AB"/("BC + CD")`
Using CD = 40 m
(BC + 40) = `"AB"sqrt3`
∴ AB = `("BC" + 40)/sqrt3` …(ii)
From (i) and (ii)
`"BC"sqrt3` = `("BC" + 40)/sqrt3`
∴ `"BC"sqrt(3) xx sqrt(3) = "BC" + 40`
∴ 3BC = BC + 40
∴ 2BC = 40
∴ BC = 20 m
Therefore width of the river = BC = 20 m
Substituting BC in equation (i)
AB = `20sqrt3`
∴ AB = 20 × 1.73
∴ AB = 34.6 m
Therefore height of tree = AB = 34.6 m
Hence height of tree is 34.6 meters and width of river is 20 meters
RELATED QUESTIONS
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 90 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
A bus travels at a certain average speed for a distance of 75 km and then travels a distance of 90 km at an average speed of 10 km/h more than the first speed. If it takes 3 hours to complete the total journey, find its first speed?
A 21 m deep well with diameter 6 m is dug and the earth from digging is evenly spread to form a platform 27 m ✕ 11 m. Find the height of the platform.[Use `pi=22/7`]
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree. (Use `sqrt(3)` = 1.732)
An electric pole is 10 m high. A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.
A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60°. to the horizontal. Find the length of the string, assuming that there is no slack in it.
[Take `sqrt(3)` =1.732 ]
Two men are on opposite side of tower. They measure the angles of elevation of the top of the tower as 30 and 45 respectively. If the height of the tower is 50 meters, find the distance between the two men.
The shadow of a tower at a time is three times as long as its shadow when the angle of elevation of the sun is 60°. Find the angle of elevation of the sun at the time of the longer shadow ?
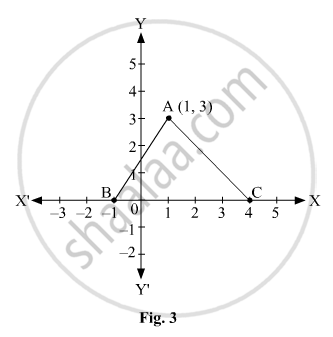
In Fig. 3, the area of triangle ABC (in sq. units) is:
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of depression from the top of the tower to the foot of the hill is 30°. If the tower is 50 m high, find the height of the hill ?
A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is
Two buildings are facing each other on a road of width 12 metre. From the top of the first building, which is 10 metre high, the angle of elevation of the top of the second is found to be 60°. What is the height of the second building ?
A storm broke a tree and the tree top rested on ground 20 m away from the
base of the tree, making an angle of 60o with the ground. Find the height
of the tree.
If the angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower in the same straight line with it are complementary, find the height of the tower.
A tree is broken by the wind. The top struck the ground at an angle of 30° and at a distance 30 m from the root. Find the whole height of the tree. (`sqrt(3)`=1.73)
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the difference between height of the lamp post and the apartment
The electric pole subtends an angle of 30° at a point on the same level as its foot. At a second point ‘b’ metres above the first, the depression of the foot of the pole is 60°. The height of the pole (in metres) is equal to
Two persons are standing ‘x’ metres apart from each other and the height of the first person is double that of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the shorter person (in metres) is
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the North of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
In given figure, the value of ZC is ____________.