Advertisements
Advertisements
प्रश्न
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is `200[(sqrt(3) + 1)/sqrt(3)]` metres, find the height of the lighthouse.
उत्तर
Let A and B the position of the first ship and the second ship
Distance = `200((sqrt(3) + 1)/sqrt(3))`m
Let the height of the lighthouse CD be h
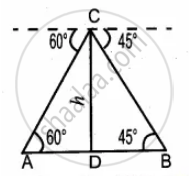
In the right ∆ACD, tan 60° = `"CD"/"AD"`
`sqrt(3) = "h"/"AD"`
∴ AD = `"h"/sqrt(3` ...(1)
In the right ∆BCD
tan 45° = `"DC"/"BD"`
1 = `"h"/"BD"`
∴ BD = h
Distance between the two ships = AD + BD
`200((sqrt(3) + 1)/sqrt3) = "h"/sqrt3 + "h"`
⇒ `200 (sqrt(3) + 1) = "h" + sqrt(3)"h"`
`200(sqrt(3) + 1) = "h"(1 + sqrt(3))`
⇒ h = `(200(sqrt(3) + 1))/((1 + sqrt(3))`
h = 200
Height of the light house = 200 m
APPEARS IN
संबंधित प्रश्न
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground, making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
A tree breaks due to the storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 10 metres. Find the height of the tree.
From the top of a tree of height 13 m the angle of elevation and depression of the top and bottom of another tree are 45° and 30° respectively. Find the height of the second tree. `(sqrt(3) = 1.732)`
If the ratio of the height of a tower and the length of its shadow is `sqrt(3): 1`, then the angle of elevation of the sun has measure
As observed from the top of a 150 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then find the width of the river.
A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high tower observes two cars at angles of depression of 30° and 60°, which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars. (use `sqrt(3)` = 1.73)
