Advertisements
Advertisements
प्रश्न
Two poles of equal heights are standing opposite to each other on either side of the road which is 80m wide, From a point P between them on the road, the angle of elevation of the top of one pole is 60 and the angle of depression from the top of another pole at P is 30 . Find the height of each pole and distance of the point P from the poles.
उत्तर

Let AB and CD be the equal poles; and BD be the width of the road.
We have,
∠AOB = 60° and ∠COD = 60°
In ΔAOB,
`tan 60° = (AB)/(BO)`
`⇒ sqrt(3) = (AB)/ (BO)`
`⇒ BO = (AB) / sqrt(3)`
Also, in ΔCOD,
`tan 30° = (CD)/(DO)`
`⇒ 1/ sqrt(3) = (CD)/(DO)`
`⇒ DO = sqrt(3)CD`
As , BD = 80
⇒ BO +DO = 80
`⇒ (AB) /sqrt(3) + sqrt(3) CD = 80`
`⇒ (AB) /sqrt(3) + sqrt(3) AB = 80` (Given : AB - CD)
`⇒AB (1/sqrt(3) + sqrt(3) ) = 80`
`⇒ AB ((1+3)/sqrt(3) )=80`
`⇒ AB (4/ sqrt(3) ) =80`
`⇒ AB = (80+sqrt(3))/4`
`⇒ AB = 20 sqrt(3) m`
`Also , BO = (AB)/ sqrt(3) = (20sqrt(3))/sqrt(3) = 20m`
So, DO = 80 - 20 = 60m
Hence, the height of each pole is 20 `sqrt(3)`m and point P is at a distance of 20 m from left pole ad 60 m from right pole.
संबंधित प्रश्न
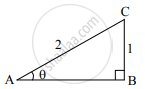
In the following figure, in ΔABC, BC = 1, AC = 2, ∠B = 90°. Find the value of sin θ.
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
The angle of elevation of a cloud from a point 60 m above the surface of the water of a lake is 30° and the angle of depression of its shadow in water of lake is 60°. Find the height of the cloud from the surface of water
From the top of a 15 m high building, the angle of elevation of the top of a tower is found to be 30°. From the bottom of the same building, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower and the distance between tower and the building.
The length of the shadow of a tower standing on the level plane is found to 2x meter longer when the sun's altitude is 30° than when it was 45°. Prove that the height of the tower is `x(sqrt3 + 1)` meters.
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
From the top of a vertical tower, the angles depression of two cars in the same straight line with the base of the tower, at an instant are found to be 45° and 60° . If the cars are 100 m apart and are on the same side of the tower, find the height of the tower.
A storm broke a tree and the treetop rested 20 m from the base of the tree, making an angle of 60° with the horizontal. Find the height of the tree.
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
A window of a house is h meters above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be A and B respectively. Then the height of the other house is ____________.
