Advertisements
Advertisements
प्रश्न
The height of a tower is 100 m. When the angle of elevation of the sun changes from 30° to 45°, the shadow of the tower becomes x metres less. The value of x is
पर्याय
100 m
\[100\sqrt{3} m\]
\[100\left( \sqrt{3} - 1 \right) m\]
\[\frac{100}{3}m\]
उत्तर
The given situation can be represented as,
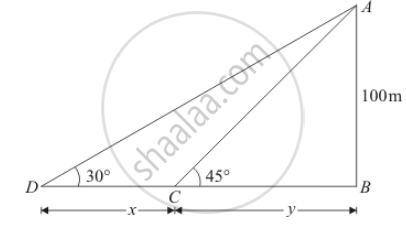
Here, AB is the tower of height 100 meters.
When angle of elevation of sun changes from`∠D=30°` to `∠C=45°`, .`CD=x`
We assumed that `BC=y`
Here we have to find the value of x
So we use trigonometric ratios.
In a triangle,`ABC`
`⇒ tan C=(AB)/(BC)`
`⇒ tan 45°=(AB)/(BC)`
`⇒1=100/y`
`⇒y=100`
Again in a triangle ABD,
`⇒ tan D=( AB)/(BC+CD)`
`⇒ tan 30°=100/(x+y)`
`⇒ 1/sqrt3=100/(x+y)`
`⇒ 100sqrt3=x+y`
`⇒100sqrt3=x+100` `Put x=100`
`⇒x=100(sqrt3-1)`
APPEARS IN
संबंधित प्रश्न
The angles of elevation and depression of the top and the bottom of a tower from the top of a building, 60 m high, are 30° and 60° respectively. Find the difference between the heights of the building and the tower and the distance between them.
A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 600 to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? `(sqrt(3) = 1.732)`
From the top of the tower 60 m high the angles of depression of the top and bottom of a vertical lamp post are observed to be 38° and 60° respectively. Find the height of the lamp post (tan 38° = 0.7813, `sqrt(3)` = 1.732)
In given figure, the value of ZC is ____________.
A TV tower stands vertically on a bank of a canal, with a height of `10 sqrt3` m. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the distance between the opposite bank of the canal and the point with a 30° angle of elevation.
If a man standing on a platform 3 meters above the surface of a lake observes a cloud and its reflection in the lake, then calculate the angle of elevation of the cloud.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are α and β, respectively. Then the height of the tower is ____________.
