Advertisements
Advertisements
प्रश्न
Two poles of equal heights are standing opposite each other an either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30º, respectively. Find the height of poles and the distance of the point from the poles.
उत्तर १
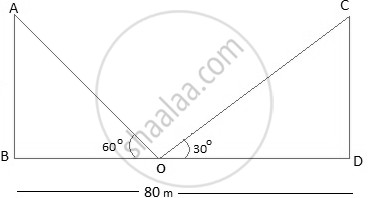
Let AB and CD be the poles and O is the point from where the elevation angles are measured.
In ΔABO
`("AB")/("BO") = tan 60°`
`("AB")/("BO") = sqrt3`
`"BO" = ("AB")/sqrt3`
In ΔCDO,
`("CD")/("DO") = tan 30°`
`("CD")/(80-"BO") = 1/sqrt3`
`"CD"sqrt3 = 80 - "BO"`
`"CD"sqrt3 = 80 - ("AB")/sqrt3`
`"CD"sqrt3+ ("AB")/sqrt3 = 80`
Since the poles are of equal heights,
CD = AB
`"CD"[sqrt3 + 1/sqrt3] = 80`
`"CD"((3+1)/sqrt3) = 80`
`"CD" = 20sqrt3`
`"BO"= ("AB")/sqrt3 = ("CD")/sqrt3`
= `((20sqrt3)/sqrt3)`m
= 20 m
DO = BD − BO
= (80 − 20) m
= 60 m
Therefore, the height of poles is `20sqrt3` and the point is 20 m and 60 m far from these poles.
उत्तर २
Let AB and CD be the two poles of equal height.
O be the point makes an angle of elevation from the top of the poles of 60° and 30°, respectively.
Let OA = 80 - x, OD = x.
And ∠BOA = 30°, ∠COD = 60°.
Here, we have to find the height of the poles and the distance of the points from the poles.
We have the corresponding figure as follows:.
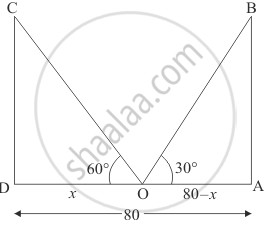
So we use trigonometric ratios.
In a triangle COD,
⇒ tan 60° = `"CD"/"DO"`
⇒ `sqrt(3) = "h"/"x"`
⇒ `"x" = "h"/sqrt(3)`
Again in a triangle AOB,
⇒ tan 30° = `"AB"/"OA"`
⇒ `(1)/sqrt(3) = "h"/(80 -"x")`
⇒ `sqrt(3)"h" = 80 - "x"`
⇒ `sqrt(3)"h" = 80 - "h"/sqrt(3)`
⇒ `sqrt(3)"h" + "h"/sqrt(3) = 80`
⇒ `3"h" + "h" = 80sqrt(3)`
⇒ `4"h" = 80sqrt(3)`
⇒ `"h" = 20sqrt(3)`
⇒ `"x" = (20sqrt(3))/sqrt(3)`
⇒ x = 20
And
⇒ OA = 80 - x
⇒ OA = 80 - 20
⇒ OA = 60
Hence, the height of pole is `20sqrt(3)` and distances are 20m, 60m respectively.
APPEARS IN
संबंधित प्रश्न
A ladder makes an angle of 60° with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is:
(A) `4/sqrt3`
(B) `4sqrt3`
(C) `2sqrt2`
(D)4
A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.

A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/h.
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
The angles of elevation of the top of a rock from the top and foot of a 100 m high tower are respectively 30° and 45°. Find the height of the rock.
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45 . If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60 , then find the height of the flagstaff [Use `sqrt(3)` 1.732]
The angles of depression of the top and bottom of a tower as seen from the top of a 60 `sqrt(3)` m high cliff are 45° and 60° respectively. Find the height of the tower.
In the following figure, what are the angles of depression from the observing position O1 and O2of the object at A?
The tops of two poles of height 16 m and 10 m are connected by a wire of length lmetres. If the wire makes an angle of 30° with the horizontal, then l =
Find the positive value of m for which the distance between the points A(5, −3) and B(13, m) is 10 units.
If the ratio of the height of a tower and the length of its shadow is `sqrt(3): 1`, then the angle of elevation of the sun has measure
The distance of point A(-5, 6) from the origin is ______.
The tops of two poles of heights 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with the horizontal, then the length of the wire is ____________.
A pole of height 30 m is observed from a point. The angle of depression of the point is 30°. Find the distance of the point from the base of the pole.
Read the following passage and answer the questions given below.
|
Kite Festival Kite festival is celebrated in many countries at different times of the year. In India, every year 14th January is celebrated as International Kite Day. On this day many people visit India and participate in the festival by flying various kinds of kites. The picture given below, show three kites flying together.
In the given figure, the angles of elevation of two kites (Points A and B) from the hands of a man (Point C) are found to be 30° and 60° respectively. Taking AD = 50 m and BE = 60 m, find. |
- the lengths of strings used (take them straight) for kites A and B as shown in the figure.
- the distance 'd' between these two kites.
An aeroplane at an altitude of 200 metres observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river. (Use = `sqrt(3)` = 1.732)
A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite bank of the river is 60° and when he retires 40 meters away from the tree the angle of elevation becomes 30°. The breadth of the river is ______.
Two circles of radii 5 cm and 3 cm touch each other externally. Find the distance between their centres.


