Advertisements
Advertisements
Question
Find the angle of elevation of the sum (sun's altitude) when the length of the shadow of a vertical pole is equal to its height.
Solution
Let θ be the angle of elevation of the sun. Let AB be the vertical pole of height h and BC be the shadow of equal length h.
Here we have to find the angle of elevation of the sun.
We have the corresponding figure as follows.
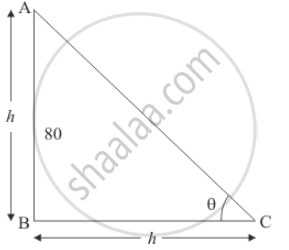
So we use trigonometric ratios to find the required angle.
In a triangle ABC
`=> tan theta = (AB/(BC)`
`=> tan theta = h/h`
`=> tan theta = 1
`=> theta = 45^@`
Hence the angle of evevation of sun is 45°
APPEARS IN
RELATED QUESTIONS
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30°. Find the distance travelled by the balloon during the interval.

A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon above the ground.
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart. the height of the light house is
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
At some time of the day, the length of the shadow of a tower is equal to its height. Then, the sun’s altitude at that time is ______.
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. The length of the tower is ____________.
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
We all have seen the airplanes flying in the sky but might have not thought of how they actually reach the correct destination. Air Traffic Control (ATC) is a service provided by ground-based air traffic controllers who direct aircraft on the ground and through a given section of controlled airspace, and can provide advisory services to aircraft in non-controlled airspace. Actually, all this air traffic is managed and regulated by using various concepts based on coordinate geometry and trigonometry.
At a given instance, ATC finds that the angle of elevation of an airplane from a point on the ground is 60°. After a flight of 30 seconds, it is observed that the angle of elevation changes to 30°. The height of the plane remains constantly as `3000sqrt(3)` m. Use the above information to answer the questions that follow-
- Draw a neat labelled figure to show the above situation diagrammatically.
- What is the distance travelled by the plane in 30 seconds?
OR
Keeping the height constant, during the above flight, it was observed that after `15(sqrt(3) - 1)` seconds, the angle of elevation changed to 45°. How much is the distance travelled in that duration. - What is the speed of the plane in km/hr.
