Advertisements
Advertisements
प्रश्न
The horizontal distance between two towers is 60 meters. The angle of depression of the top of the first tower when seen from the top of the second tower is 30° . If the height of the second tower is 90 meters. Find the height of the first tower.
उत्तर
Let DE be the first tower and AB be the second tower.
Now, AB = 90 m and AD = 60 m such that CE = 60 m and ∠BEC = 30°.
Let DE = h m such that AC = h m and BC = (90- h)m.
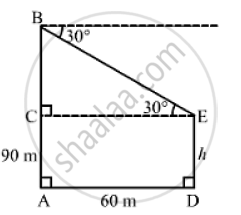
In the right ΔBCE,we have:
`(BC)/(CE) = tan 30° = 1/ sqrt(3)`
`⇒ ((90-h )) /60 = 1/ sqrt(3) `
`⇒ (90-h ) sqrt(3) = 60`
`⇒ h sqrt(3) = 90 sqrt( 3 ) -60`
`⇒ h = 90- 60/ sqrt(3) = 90- 34.64 = 55.36 m`
∴ Height of the first tower = DE = h = 55.36m
APPEARS IN
संबंधित प्रश्न
When the sun is 30º above the horizontal, Find the length of shadow cast by a building 50m high
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
The vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height 6m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is
30 and that of the top of the flagstaff 60 . Find the height of the tower
[Use `sqrt(3)` 1.732 ]
From the top of a hill, the angles of depression of two consecutive kilometer stones due east are found to be 45° and 30° respectivly. Find the height of the hill ?
The radius (in cm) of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45º. Then the height of the tower (in metres) is
To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? `(sqrt(3) = 1.732)`
A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h(1+ tan α tan β) metres.
Two poles of heights 25 m and 35 m stand vertically on the ground. The tops of two poles are connected by a wire, which is inclined to the horizontal at an angle of 30°. Find the length of the wire and the distance between the poles.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30°. Determine the height of the tower.
