Advertisements
Advertisements
प्रश्न
The angle of elevation of a tower from a point on the same level as the foot of the tower is 30°. On advancing 150 metres towards the foot of the tower, the angle of elevation of the tower becomes 60°. Show that the height of the tower is 129.9 metres (Use `sqrt3 = 1.732`)
उत्तर
Let h be the height of tower and angle of elevation of the foot of the tower is 30°, on advancing 150 m towards the foot of tower then an angle of elevation becomes 60°.
We assume that BC = x and CD = 150 m.
Now we have to prove height of the tower is 129.9 m.
So we use trigonometrical ratios.
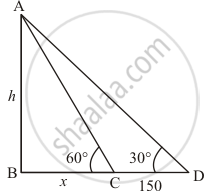
In a triangle ABC
`=> tan C = (AB)/(BC)`
`=> tan 60^@ = (AB)/(BC)`
`=> sqrt3 = h/x`
`=> h/sqrt3 = x`
Again in a triangle ABD
`=> tan D = (AB)/(BC + CD)`
`=> tan 30^@ = h/(x + 150)`
`=> 1/sqrt3 = h/(x + 150)`
`=> x + 150 = sqrt3h`
`=> x = sqrt3h - 150`
`=> h/sqrt3 = sqrt3 - 150`
`=> h = 3h - 150sqrt3`
`=> 2h = 150sqrt3`
`=> h = (150 xx 1.732)/2`
=> h = 129.9
Hence the height of tower is 129.9 m proved
APPEARS IN
संबंधित प्रश्न
A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of a hill as 30°. Find the distance of the hill from the ship and the height of the hill
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 45°. If the tower is 30 m high, find the height of the building.
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
The angle of elevation of the top of a tower from a point A on the ground is 30°. Moving a distance of 20metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower & the distance of the tower from the point A.
A carpenter makes stools for electricians with a square top of side 0.5 m and at a height of 1.5 m above the ground. Also, each leg is inclined at an angle of 60° to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances.
From the point of a tower 100m high, a man observe two cars on the opposite sides to the tower with angles of depression 30° and 45 respectively. Find the distance between the cars
A man on the deck of a ship, 16m above water level, observe that that angle of elevation and depression respectively of the top and bottom of a cliff are 60° and 30° . Calculate the distance of the cliff from the ship and height of the cliff.
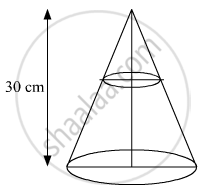
In fig. 9 is shown a right circular cone of height 30 cm. A small cone is cut off from the top by a plane parallel to the base. If the volume of the small cone is 127127 of the volume of cone, find at what height above the base is the section made.
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
