Question

Two ships are approaching a light-house from opposite directions. The angles of depression of the two ships from the top of the light-house are 30° and 45°. If the distance between the two ships is 100 m, find the height of the light-house. \[[Use \sqrt{3} = 1 . 732]\]

Answer 1

Let h be the height of the light house.
Let us suppose that the distance of one of the ships from the light house is x metres. Then, the distance of the other ship from the light house will be 100 − x metres.

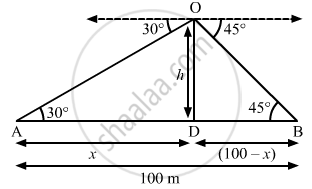
In right-angled triangle ADO, we have:

\[\tan {30}^\circ = \frac{OD}{AD} = \frac{h}{x}\]
\[ \Rightarrow \frac{1}{\sqrt{3}} = \frac{h}{x}\]
\[ \Rightarrow x = \sqrt{3}h . . . (1)\]

In right-angled triangle BDO, we have:

\[\tan {45}^\circ = \frac{OD}{BD} = \frac{h}{100 - x}\]
\[ \Rightarrow 1 = \frac{h}{100 - x}\]
\[ \Rightarrow x + h = 100\]
\[\text{On putting x} = \sqrt{3}h, \text{we get}: \]
\[\sqrt{3}h + h = 100\]
\[ \Rightarrow h\left( \sqrt{3} + 1 \right) = 100\]
\[ \Rightarrow h = \frac{100}{\sqrt{3} + 1}\]
\[ \Rightarrow h = \frac{100}{\left( \sqrt{3} + 1 \right)} \times \frac{\left( \sqrt{3} - 1 \right)}{\left( \sqrt{3} - 1 \right)}\]
\[ \Rightarrow h = \frac{100}{2}\left( \sqrt{3} - 1 \right)\]
\[ \Rightarrow h = 36 . 6 (\text{approx} . )\]

Thus, the height of the light house is approximately 36.6 m.